Question 634705: Multiply the rational expression.
(16a+8)/(5a^2+5)*(2a^2+a-1)/(4a^2-1)
Show step-by-step, please.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm assuming that the expression is:
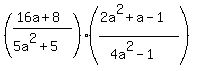
and not
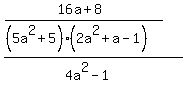
and not

You did well to put the numerators and the denominators in parentheses. It would help to put the whole fractions in parentheses, too:
((16a+8)/(5a^2+5))*((2a^2+a-1)/(4a^2-1))
Back in the "good old days", when numerators and denominators were simple whole numbers, you should have learned that when you are multiplying fractions...- It was OK to cancel factors before you multiplied.
- Cross-canceling, canceling a factor in one fraction's numerator with the same factor in another fraction's denominator, was OK, too.
- In fact, not only was it OK but it was a very good idea to cancel as much as possible before you multiplied. It made the rest of the problem much easier.
For example:
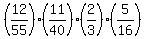
Factoring we get:
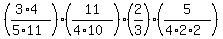
Canceling:

leaving:
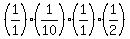
which, you must agree, will be much eaier to multiply than what we started with. Plus, we've already done all the canceling. We will not have to reduce the answer we get.
The reason I went through all that was to make this point: With fractions like we have in this problem:
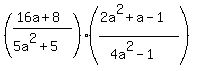
is more important and more useful than ever before that we try to cancel before we go ahead and multiply. So we start with factoring so we can see what will cancel, if anything:

And we do indeed get some factors we can cancel:
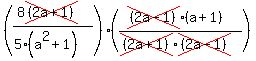
leaving
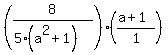
This is clearly easier to multiply than what we started with. Multiplying this out we get:

|
|
|