Question 624418: solve:X^3-4X^2+4X+48=0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve an equation like this one would normally factor it. But if the expression you posted does not factor:- The greatest common factor of
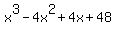 is 1 (which we rarely bother factoring out). is 1 (which we rarely bother factoring out). 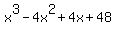 has too many terms for any of the factoring patterns. has too many terms for any of the factoring patterns.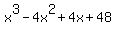 has too many terms for trinomial factoring has too many terms for trinomial factoring- I can see no way to factor it by grouping.
- The possible rational roots of
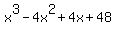 are: are:
1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 8, -8, 12, -12, 16, -16, 24, -24, 48 and -48
But none of these are roots.
If there was an error in what you posted then re-post your problem. If there were no errors, then keep reading...
Below are two graphs of  gives you a high-level view showing the "interesting" parts of the graph and the second one uses a differnt scale on the x-axis. This gives us a horizontally stretched view so we can better see some of the features of the graph, especially the x-intercept). (The x-intercept(s) would be the solution to your equation because x-intercepts have y values that are zero.) gives you a high-level view showing the "interesting" parts of the graph and the second one uses a differnt scale on the x-axis. This gives us a horizontally stretched view so we can better see some of the features of the graph, especially the x-intercept). (The x-intercept(s) would be the solution to your equation because x-intercepts have y values that are zero.)
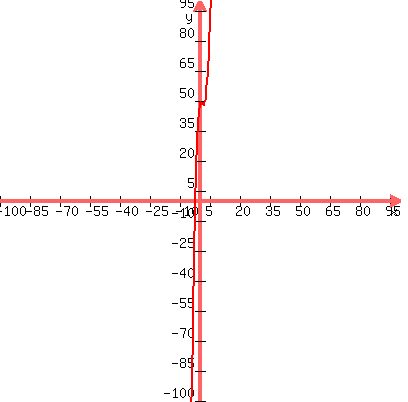
As you can see from this high-level view, the graph crosses the x-axis just once. This means that there is only one real solution to your equation. (Note: The graph does not "bend around" and come back to cross the x-axis outside of what we see here.)
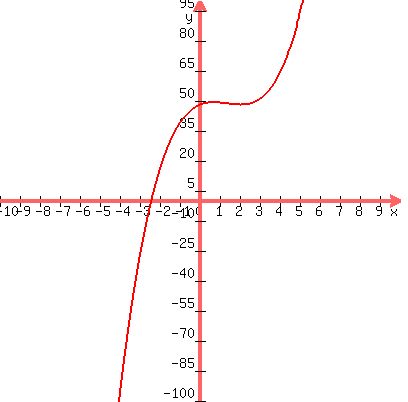
As you can see from this stretched view, the graph crosses the x-axis somewhere between -2 and -3. None of the possible rational roots were between -2 and -3. This tells us that the one real solution is an irrational number between -2 and -3.
There is a formula for cubic equations but it is very complex and not often taught in Math classes. Click here if you want to see it.
If you have a graphing calculator and know how to use its trace function. you could find a decimal approximation for the solution to your equation. Just trace to the x-intercept.
|
|
|