SOLUTION: Solve (x-1)(x+4)<0

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Solve (x-1)(x+4)<0      Log On


   

Question 620182: Solve (x-1)(x+4)<0
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
(x-1)(x+4)<0 | Change < to = and find the zeroes by solving for x (each factor).


x=1, x=-4 |Set up and test intervals based on those zeroes: x < -4, -4 < x < 1, x > 1


x < -4, choose -4: (-5-1)(-5+4) = -6*-1 = 6 which is not < 0. This interval doesn't work.


-4 < x < 1, choose 0: (0-1)(0+4) = -1*4 = -4 < 0. This interval works.


x >1, choose 2: (2-1)(2+4) = 1*6 = 6 not < 0. This interval doesn't work.


The answer is -4 < x < 1.


If you know parabolas, or graph this, you will see this is less than 0 between the zeroes. Check out the graph (at the bottom).

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B3x%2B-4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%283%29%5E2-4%2A1%2A-4=25.

Discriminant d=25 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-3%2B-sqrt%28+25+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%283%29%2Bsqrt%28+25+%29%29%2F2%5C1+=+1
x%5B2%5D+=+%28-%283%29-sqrt%28+25+%29%29%2F2%5C1+=+-4

Quadratic expression 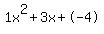1x%5E2%2B3x%2B-4 can be factored:
1x%5E2%2B3x%2B-4+=+1%28x-1%29%2A%28x--4%29
Again, the answer is: 1, -4. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B3%2Ax%2B-4+%29


Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)