Question 613871: what are the rational zeroes and all real zeroes for 4x^3-11x^2+10x-3
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!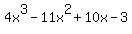 
The zeroes of a polynomial are the value(s) of the variable that make the polynomial evaluate to a zero. So when a problem like this is asking for the zeroes it is, in other words, asking you to solve:
To solve an equation like this, with an exponent higher than 2, you start by getting side of the equation to be zero and then factoring. Our equation already has one side that is zero so we can go straight to the factoring.
Always start factoring by factoring out the greatest common factor, GCF, (unless it is 1). The GCF here is 1 so we move on to other methods of factoring.
The factoring patterns all have 2 or 3 terms in them. Our equation as 4 terms on the left side. So we cannot use the patterns.
Trinomial factoring is for 3-term expressions. So again we have too many terms for this method.
Factoring by grouping requires an even number of terms. We have an even number of terms so this may work for us. But I do not yet see an easy way for this to work for us. So I'm going on to...
Factoring by trial and error of the possible rational roots. This method, as the name implies, often involves a lot of trial and error. So I usually use this method as a method of last resort. Well, we're there. We've tried all the other methods and nothing works (unless a very complex factoring by grouping turns out to work).
The possible rational roots of a polynomial are all the possible ratios, positive and negative, that can be formed by a factor of the constant term (at the end) over a factor of the leading coefficient (in front of the highest power term). Your constant term is -3 so its factors are 1 and 3. (We will be using both all positive and negative ratios so we do not need to be concerned about the fact that one factor of -2 is negative and the other positive.) Your leading coefficient is 4, whose factors are 1, 2 and 4. So the possible rational roots for our polynomial are:
1/1 (or 1), -1/1 (or -1), 3/1 (or 3), -3/1 (or -3), 1/2, -1/2, 3/2, -3/2, 1/4, -1/4, 3/4 and -3/4
This is quite a long list of possible rational roots. It could take some time to find out which of these, if any, are actual roots. Let's hope this goes quickly. Since 1 is a factor of everything, it always turns out to be one of the possible rational roots of a polynomial. and since raising 1 to different powers is very easy, it is very easy to check if 1 is a root. Since 1 to any power is 1 and since we know how multiplying by 1 works, our equation becomes, when x = 1:
4 - 11 + 10 - 3 = 0
and this is actually true!! So 1 is a root!
Now we continue to look for the other roots. We could continue to try the other possible rational roots. But we have a better option. Since 1 is a root, it means that (x-1) is a factor of the polynomial. The other roots we are looking for will be the roots of the "other" factor. This other factor will have a lower degree and it may have a smaller list of possible roots. So if we can find this other factor, our path is easier than continuing to try those rational roots.
To find the other factor, we divide the polynomial by (x-1). And the easiest way to divide is to use synthetic division (which I hope you have learned):
1 | 4 -11 10 -3
=== 4 -7 3
==================
4 -7 3 0
The remainder is the number in the lower right corner. It is zero (which we expected since we already knew (x-1) was a factor). The rest of the bottom row tells us the other factor. The "4 -7 3" translates into 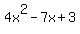 . And the roots we have yet to find are roots of .
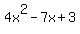Since 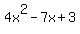is a quadratic (with 3 terms) we can use some of the other factoring methods we had to skip when we had 4 terms to factor. This quadratic will factor, using trinomial factoring, into:
(x-1)(4x-3)
We have now fully factored :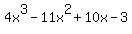
Note that (x-1) is a factor twice. We found one of them when we were trying the rational roots and we found another factor of (x-1) when we factored .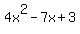
With the factors we can find all the roots. Just set each factor to zero and solve:
x-1 = 0 or x-1 = 0 or 4x-3 = 0
Solving these we get:
x = 1 or x = 1 or x = 3/4.
This makes the three roots of :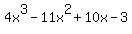
1, 1 and 3/4
All three are rational and, since all rationals are real, all three are real roots.
Note 1: The 1 counts twice as a root since (x-1) is a factor twice. This is called a "double root" or "a root of multiplicity 2".
Note 2: If we had continued the trial and error of the rational roots after finding the first one (instead of factoring 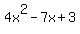), we may- have never figured out that 1 was a double root; and/or
- have taken a long tine before we finally got around to trying 3/4 as a rational root.
|
|
|
