|
Question 613365: l.c.m. for
10m^2-40, 5m+10
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! A reliable way to find LCM's is to factor each number/expression fully. This includes factoring numbers down to prime factors.
Factoring 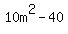 : :
First the GCF of 10:

The prime factors of 10 are 5 and 2. And the other factor is a difference of squares which will factor according to the  pattern. So pattern. So 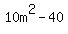 , fully factored is: , fully factored is:
5*2*(m+2)(m-2)
Factoring 5m+10:
first the GCF:
5(m+2)
Next, it can be helpful to list the factors in a certain way:
10m^2-40 = 5 * 2 * (m+2) * (m-2)
5m+10 = 5 (m+2)
Note how I lined up the matching factors. If 5m+10 had another factor that did not match a factor from 10m^2-40, it would have been listed out at the end, in its own column. The LCM will get a factor from each separate column:
10m^2-40 = 5 * 2 * (m+2) * (m-2)
5m+10 = 5 (m+2)
LCM = 5 * 2 * (m+2) * (m-2)
Again, if the 5m+10 had had another, different factor (which would be in its own column), then it would be included in the LCM, too!
As we can see, the LCM factors are exactly the same as those for 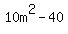 . So the LCM is . So the LCM is 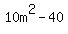 . .
Another reason this method of finding LCM's is handy is that it is easy to see what factors one of the original expression is "missing". For example, one use of LCM's is to match denominators of fractions so you can add or subtract them. If we had:
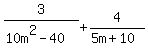
We would find the LCM of the denominators and then change the fractions so they had the LCM as their denominators. Since the first fraction already has the LCM as its denominator it is fine as it is. The second denominator needs to change. And we can see from
5m+10 = 5 (m+2)
LCM = 5 * 2 * (m+2) * (m-2)
that 5m+10 is "missing" a factor of 2 and a factor of (m-2). So these are what we need to use to change the denominator to the LCM:
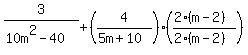
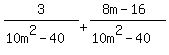
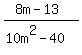
|
|
|
| |