Question 606433: Hi, were working on factoring right now in class. We've factored the trinomial but now we are working on functions and I'm lost can you help please?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If you are still factoring, then your functions are still polynomials.
Or maybe there is one (or more) easy binomial factor(s), whose constant/independent term is/are a factor of your long polynomials's independent term.
Maybe you are beyond polynomials, but you are now studying rational functions, meaning one polynomial divided by another.
When dealing with polynomials that are longer than trinomials, you know that they will be of degree 3 or higher. Those are trickier to factor, but if your teacher expects you to be able to factor them, there must be a way. They could be the cube of a binomial, or some other known special product, like
 or 
Or maybe you can factor by grouping.
When dealing with rational functions, you still have to factor (if possible) the numerator and denominator of your rational function. If possible, you simplify, understanding that zeros of the original denominator are excluded from the domain of the function, and zeros of the simplified rational function denominator are vertical asymptotes.
So  = 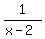when x is not zero, and it is undefined for x=0 (a hole). And x=2 is a vertical asymptote (also excluded from the domain).
So,  has a hole at x=0, and a vertical asymptote at x=2.
That's as far as I can help without talking further. If you enter a thank you on the website, the website will give me your email address. Unless that happens, we both keep private and uncommunicated, but you could still ask other, more specific questions.
|
|
|
