Question 579150: find zeros and multiplicities
a) f(x)= x^3-12x^2-55x+150
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is a polynomial is a polynomial
We know that if it has a rational zero, it will be a "fraction" whose denominator is a factor of the leading coefficient and whose numerator is a factor of the constant (or independent term, whatever you call it), with a plus or minus sign in front.
The leading coefficient (the coefficient of the term of highest degree) is that invisible 1 in front of  . So the denominator is a factor of 1, which could only be 1. Any rational zero will be an integer. It has to be a factor of 150. There are 12 positive factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30,7 5, and 150. The same numbers with a minus sign in front are also possibilities. I tried 1, and it was not a zero, but then I tried 2, and 2 was a zero. . So the denominator is a factor of 1, which could only be 1. Any rational zero will be an integer. It has to be a factor of 150. There are 12 positive factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30,7 5, and 150. The same numbers with a minus sign in front are also possibilities. I tried 1, and it was not a zero, but then I tried 2, and 2 was a zero.
Since 2 is a zero of  , ,  is a factor of is a factor of  . .  can be evenly divided by can be evenly divided by  . .
I did the division and the result was 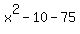 . So . So

Factoring 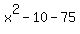 , I found that , I found that 
So  and its zeros are x=2, x=15, and x=-10. and its zeros are x=2, x=15, and x=-10.
|
|
|