Question 57317: factoring trinomials by grouping
6c^3+c^2-7c
Found 2 solutions by stanbon, funmath:
Answer by stanbon(75887)   (Show Source): (Show Source):
Answer by funmath(2933)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form of a quadratic equation is:  , when I refer to a, I mean the coefficient of x^2, when I say b, I mean the coefficient of x, and when I say c, I am referring to the number without an x. , when I refer to a, I mean the coefficient of x^2, when I say b, I mean the coefficient of x, and when I say c, I am referring to the number without an x.
factoring trinomials by grouping
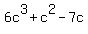
First factor out your GCF,c.
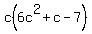
Now we need to replace b with two numbers that multiply together to give you a*c but add together to give you b.
Our a=6, b=1, and c=-7 and a*c=6(-7)=-42
Two numbers that multiply to get -42, but add to get 1 are: 7 and -6
7*-6=-42 and 7-6=1
Replace c with 7c-6c
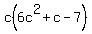
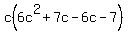 Group the first two terms and the second two terms Group the first two terms and the second two terms
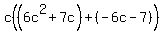 Factor the GCF out of each parenthesis. Factor the GCF out of each parenthesis.
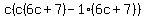 Factor out (6c+7) because both c and -1 have that as a cofactor. Factor out (6c+7) because both c and -1 have that as a cofactor.
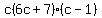
Happy Calculating!!!!
|
|
|