Question 490772: Factor 4x^2 – 14x – 8
There are no numbers whose sum is -14 and can multiple to make 4... I feel like I'm missing something?
Found 2 solutions by John10, MathTherapy:
Answer by John10(297)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hint: apply the formula (x - a)(x - b) = 0 where a and b are the solutions
Find the solutions first by using the quadratic formula. Then you plug the solution into above formula.
John10:)
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website! Factor 4x^2 – 14x – 8
There are no numbers whose sum is -14 and can multiple to make 4... I feel like I'm missing something?
Yes, you are missing something. The sum needs to be - 14, but the product is not 4, but - 32 (c * a, or - 8 * + 4) instead. However, before you factor this trinomial, you would need to first find and use its GCF, as follows:
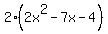
Now, as you can see, we have to find two factors whose sum is - 7, and whose product is - 8 (c * a, or - 4 * + 2). These two factors are: - 8 and + 1
We now have: 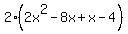 ----- 2[2x(x - 4) + 1(x - 4)] ---- ----- 2[2x(x - 4) + 1(x - 4)] ---- 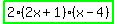
|
|
|