Question 446771: (y^2-4/y+3)=2-(y-2/y+3)
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! (y^2-4/y+3)=2-(y-2/y+3)
(y^2-4/y+3)+(y-2/y+3)=2
multiply by (y+3)
y^2-4+y-2=2(y+3)
y^2+y-6=2y+6
y^2-y-12=0
y^2-4y+3y-12=0
y(y-4)+3(y-4)=0
(y-4)(y+3)=0
y=4 OR -3
Answer by ikleyn(53419)  (Show Source):
You can put this solution on YOUR website! .
(y^2-4/y+3) = 2-(y-2/y+3)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As it is written in the post, it is inaccurate writing and it does not correspond to real intent.
The correct equation is
 =  .
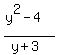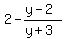Now, @mananth gives the solutions y = 4 OR y = -3.
But if you will present it in this form to your teacher, you can easily get the score of '2'.
It is because y = -3 IS NOT a solution. It is not even in the domain of this equation.
Therefore, the solution to this problem should start with these words
The domain of this equation is the set of all real numbers except of y = -3,
because (y+3) is in the denominator of the formulas.
After that, you make all this analysis, which @mananth makes, but at the end you say
Since the root y = -3 is out of the domain, the only solution to the given equation is y = 4.
It is how to present the complete solution correctly and to get the highest score.
|
|
|
