SOLUTION: m to the 2nd power, -12m+5 can you help me solve and show me how. Thank you

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: m to the 2nd power, -12m+5 can you help me solve and show me how. Thank you      Log On


   

Question 420691: m to the 2nd power, -12m+5 can you help me solve and show me how. Thank you
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Since "<" is SHIFT+comma, I have to assume that the comma is supposed to be a "<", making your problem:
m%5E2+%3C+-12m+%2B+5
Solving this quadratic inequality is much like solving a quadratic equation. We start by making one side zero. Since the rest of the problem will be a little easier if the coefficient of the squared term is positive, I am going to subtract the entire right side of the inequality from each side giving us:
m%5E2+%2B+12m+-5+%3C+0
Next we will find the x's that make m%5E2+%2B+12m+-5 zero. IOW, we will solve:
m%5E2+%2B+12m+-5+=+0
This does not factor (easily) so we will use the Quadratic Formula:
m+=+%28-%2812%29+%2B-+sqrt%28%2812%29%5E2+-+4%281%29%28-5%29%29%29%2F2%281%29
which simplifies as follows:
m+=+%28-%2812%29+%2B-+sqrt%28144+-+4%281%29%28-5%29%29%29%2F2%281%29
m+=+%28-%2812%29+%2B-+sqrt%28144+%2B+20%29%29%2F2%281%29
m+=+%28-%2812%29+%2B-+sqrt%28164%29%29%2F2%281%29
m+=+%28-12+%2B-+sqrt%28164%29%29%2F2
m+=+%28-12+%2B-+sqrt%284%2A41%29%29%2F2
m+=+%28-12+%2B-+sqrt%284%29%2Asqrt%2841%29%29%2F2
m+=+%28-12+%2B-+2%2Asqrt%2841%29%29%2F2
m+=+%282%28-6+%2B-+sqrt%2841%29%29%29%2F2
m+=+%28cross%282%29%28-6+%2B-+sqrt%2841%29%29%29%2Fcross%282%29
m+=+-6+%2B-+sqrt%2841%29
In long form this is:
m+=+-6+%2B+sqrt%2841%29 or m+=+-6+-+sqrt%2841%29
So these two values will make m%5E2+%2B+12m+-5+=+0. And if that is true, then we can use these values to write m%5E2+%2B+12m+-5 in factored form:
%28m+-+%28-6+%2B+sqrt%2841%29%29%29%28m+-+%28-6+-+sqrt%2841%29%29%29
If this is not clear to you then think of this:
  • If m = -6+%2B+sqrt%2841%29 then won't the first factor be -6+%2B+sqrt%2841%29 - -6+%2B+sqrt%2841%29?
  • And if you subtract something from itself, don't you get zero?
  • And if a factor is zero, doesn't the entire product become zero?
The same reasoning can be applied to the other factor, too.

Returning to the inequality, we can now write it in factored form:
%28m+-+%28-6+%2B+sqrt%2841%29%29%29%28m+-+%28-6+-+sqrt%2841%29%29%29+%3C+0
This inequality says that the product of two factors is less than zero. IOW: the product of two factors is negative. And how do we get a negative when multiplying two factors? Well two positive factors and two negative factors will result in a positive product. And if either factor is zero then the product is zero. So the only way for the product to be negative is if one factor is positive and one is negative.

So the solution for your inequality will be the m's that make one of the factors positive and the other factor negative. To figure out what these m's are, think of the following: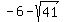
  • -6+%2B+sqrt%2841%29%29%29 is larger than -6+-+sqrt%2841%29%29%29 (since we add the square root in the first one and subtract the square root in the second one)
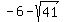  • Picture a number line with these numbers on it -6+%2B+sqrt%2841%29%29%29 and -6+-+sqrt%2841%29%29%29. The first one, being larger, will be to the right of the second one.
  • Think of the number line being divided into three parts:
    • The "far left" which is to the left of both of these numbers (i.e. to the left of the lower number),
    • The "far right" which is to the right of both numbers (i.e. to the right of the higher number).
    • And "in between"
  • The m's in the "far left" part will make both factors negative (and the product positive.
  • The m's in the "far right" part will make both factors positive (and the product positive).
  • The m's in the "in between" part will make one factor positive and one negative (and the product negative. These are the m's we are looking for.

So the solution is all the numbers between 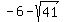-6+-+sqrt%2841%29%29%29 and -6+%2B+sqrt%2841%29%29%29. In other "words":
-6+-+sqrt%2841%29+%3C+m+%3C+-6+-+sqrt%2841%29