Question 407841: factoring 3x^2-5x-884
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Looking at 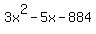 we can see that the first term is we can see that the first term is  and the last term is and the last term is 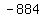 where the coefficients are 3 and -884 respectively. where the coefficients are 3 and -884 respectively.
Now multiply the first coefficient 3 and the last coefficient -884 to get -2652. Now what two numbers multiply to -2652 and add to the middle coefficient -5? Let's list all of the factors of -2652:
Factors of -2652:
1,2,3,4,6,12,13,17,26,34,39,51,52,68,78,102,156,204,221,442,663,884,1326,2652
-1,-2,-3,-4,-6,-12,-13,-17,-26,-34,-39,-51,-52,-68,-78,-102,-156,-204,-221,-442,-663,-884,-1326,-2652 ...List the negative factors as well. This will allow us to find all possible combinations
These factors pair up and multiply to -2652
(1)*(-2652)
(2)*(-1326)
(3)*(-884)
(4)*(-663)
(6)*(-442)
(12)*(-221)
(13)*(-204)
(17)*(-156)
(26)*(-102)
(34)*(-78)
(39)*(-68)
(51)*(-52)
(-1)*(2652)
(-2)*(1326)
(-3)*(884)
(-4)*(663)
(-6)*(442)
(-12)*(221)
(-13)*(204)
(-17)*(156)
(-26)*(102)
(-34)*(78)
(-39)*(68)
(-51)*(52)
note: remember, the product of a negative and a positive number is a negative number
Now which of these pairs add to -5? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to -5
| First Number | Second Number | Sum | | 1 | -2652 | 1+(-2652)=-2651 | | 2 | -1326 | 2+(-1326)=-1324 | | 3 | -884 | 3+(-884)=-881 | | 4 | -663 | 4+(-663)=-659 | | 6 | -442 | 6+(-442)=-436 | | 12 | -221 | 12+(-221)=-209 | | 13 | -204 | 13+(-204)=-191 | | 17 | -156 | 17+(-156)=-139 | | 26 | -102 | 26+(-102)=-76 | | 34 | -78 | 34+(-78)=-44 | | 39 | -68 | 39+(-68)=-29 | | 51 | -52 | 51+(-52)=-1 | | -1 | 2652 | -1+2652=2651 | | -2 | 1326 | -2+1326=1324 | | -3 | 884 | -3+884=881 | | -4 | 663 | -4+663=659 | | -6 | 442 | -6+442=436 | | -12 | 221 | -12+221=209 | | -13 | 204 | -13+204=191 | | -17 | 156 | -17+156=139 | | -26 | 102 | -26+102=76 | | -34 | 78 | -34+78=44 | | -39 | 68 | -39+68=29 | | -51 | 52 | -51+52=1 |
None of these pairs of factors add to -5. So the expression 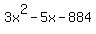 cannot be factored cannot be factored
In other words, the polynomial is prime.
If you need more help, email me at jim_thompson5910@hotmail.com
Also, please consider visiting my website: http://www.freewebs.com/jimthompson5910/home.html and making a donation. Thank you
Jim
|
|
|