Question 362021: I'm still trying to finish this packet I have... So here's another few questions I'm having a hard time with.
I really appreciate the help, and I reallyyy need it!
1. r to the third + r^ - 6r
2. x^ - 14x + 49
x^ + 1 over 2x + 1 over 16
(as fractions)
3. 81m to the fourth - 16
4. 4- 2q - 6p + 3pq
5. 3n to the third + 12n^ - 36n
6. r^ + r + 3
7. 16x^ - 14x + 3
8. 7b^ - 42b + 56
9. y^ + 4y - 45
10. 8a^ + 23a - 3
Thank you againnn! I just really need to get this class out of my way. It's holding me back from continuing other work and classes that I don't even struggle with. I'm sure you can imagaine my frustration with this! But thank you for the help...
Answer by JBarnum(2146)   (Show Source): (Show Source):
You can put this solution on YOUR website! these are mostly quadratic equations(1,2,5,6,7,8,9,10) which are solved the same way you just need to do the calculations i will do one equation for u below:
#1
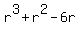
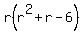
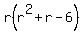 +3 and -2 are two numbers that multiply to get -6 and add to get +1, if you cant do it this way use the quadratic formula to solve. +3 and -2 are two numbers that multiply to get -6 and add to get +1, if you cant do it this way use the quadratic formula to solve.
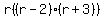
 = =
 = =
#3
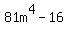
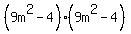

 = =
 = =
#4 Im not sure what the question is asking for you to do, cause u cant find what either equals with 2 variables makes near unlimited possible solutions
#10

| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=625 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 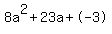 can be factored: can be factored:

Again, the answer is: 0.125, -3.
Here's your graph:
 |
|
|
|