Question 334877: I found the possible rational roots for 4x^4+8x^3-x^2-14x-24 are 1/2,1,2,3,4,6,8,12 (postive and negative). My question is how can I find the actual rational roots? Do I need to plug them in to see which ones work? Or is there an easier way to do this?
Thank you so much!!
Found 2 solutions by vleith, Edwin McCravy:
Answer by vleith(2983)   (Show Source): (Show Source):
You can put this solution on YOUR website! Plug in until you find one. Know that you may not find any (especially for polynomials of even degree.
Then you can either keep trying trial and error or use long division to divide by the number that is a root. The result will be a polynomial of degree one less than the original polynomial. Then you can either plug and play there or use some other means to find out the other factors.
A good way to check long division is with this online tool
http://www.calc101.com/webMathematica/long-divide.jsp
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
You can put this solution on YOUR website! I found the possible rational roots for 4x^4+8x^3-x^2-14x-24 are 1/2,1,2,3,4,6,8,12 (postive and negative). My question is how can I find the actual rational roots? Do I need to plug them in to see which ones work? Or is there an easier way to do this?
First of all you don't have all the candidates for rational roots,
for 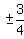 and and 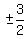 are also candidates for rational roots.
You can use DesCartes' rule of signs. There is only one sign change
from left to right, so you know there is one positive root. You might
try to find it, since it might be rational (though it might not be!).
Try the easiest, 1:
1 | 4 8 -1 -14 -24
| 4 12 11 -3
4 12 11 -3 -27
Nope!
Try the next easiest, 2:
2 | 4 8 -1 -14 -24
| 8 32 62 96
4 16 31 48 72
Now we know there is no need to try any
larger number than 2, because all the numbers
on the bottom are positive. That means
2 is an UPPER BOUND to the positive roots.
Also since the remainder was negative (-27) when
we tried 1 and positive (72) when we tried 2, that
the positive root is between those two. The
only candidate for a rational root between those
is 3/2, which you left out!!!
3/2 | 4 8 -1 -14 -24
| 6 21 30 24
4 14 20 16 0
Hurray! We have found a root are also candidates for rational roots.
You can use DesCartes' rule of signs. There is only one sign change
from left to right, so you know there is one positive root. You might
try to find it, since it might be rational (though it might not be!).
Try the easiest, 1:
1 | 4 8 -1 -14 -24
| 4 12 11 -3
4 12 11 -3 -27
Nope!
Try the next easiest, 2:
2 | 4 8 -1 -14 -24
| 8 32 62 96
4 16 31 48 72
Now we know there is no need to try any
larger number than 2, because all the numbers
on the bottom are positive. That means
2 is an UPPER BOUND to the positive roots.
Also since the remainder was negative (-27) when
we tried 1 and positive (72) when we tried 2, that
the positive root is between those two. The
only candidate for a rational root between those
is 3/2, which you left out!!!
3/2 | 4 8 -1 -14 -24
| 6 21 30 24
4 14 20 16 0
Hurray! We have found a root  , and x- , and x- is a factor
So now you have factored the original polynomial as
(x - is a factor
So now you have factored the original polynomial as
(x -  )(4x³ + 14x² + 20x +16)
and you can factor a 2 out of that cubic polynomial
(x - )(4x³ + 14x² + 20x +16)
and you can factor a 2 out of that cubic polynomial
(x -  )2(2x³ + 7x² + 10x + 8)
or
2(x - )2(2x³ + 7x² + 10x + 8)
or
2(x -  )(2x³ + 7x² + 10x + 8)
So now we are working with only the cubic polynomial:
2x³ + 7x² + 10x + 8
It has no sign changes so it has no positive roots.
So its candidates for rational roots are only negatives:
-1/2, -1, -2, -3, -4, -8
We try the easiest, -1
-1 | 2 7 10 8
| -2 -5 -5
2 5 5 3
Nope!
[Note: the rule for LOWER bounds on negative roots is
not the same as the rule for UPPER bounds on positive
roots, for the signs on the bottom have to ALTERNATE
in order to know that we have a LOWER bound.]
We try the next easiest, -2
-2 | 2 7 10 8
| -4 -6 -8
2 3 4 0
Hurray! We have found another root -2, and x+2 is a factor
So we have now factored the original polynomial as
2(x - )(2x³ + 7x² + 10x + 8)
So now we are working with only the cubic polynomial:
2x³ + 7x² + 10x + 8
It has no sign changes so it has no positive roots.
So its candidates for rational roots are only negatives:
-1/2, -1, -2, -3, -4, -8
We try the easiest, -1
-1 | 2 7 10 8
| -2 -5 -5
2 5 5 3
Nope!
[Note: the rule for LOWER bounds on negative roots is
not the same as the rule for UPPER bounds on positive
roots, for the signs on the bottom have to ALTERNATE
in order to know that we have a LOWER bound.]
We try the next easiest, -2
-2 | 2 7 10 8
| -4 -6 -8
2 3 4 0
Hurray! We have found another root -2, and x+2 is a factor
So we have now factored the original polynomial as
2(x -  )(x + 2)(2x² + 3x + 4)
The quadratic will not factor so we have to use the
quadratic formula to find the other two roots, by
setting the quadratic equal to zero:
2x² + 3x + 4 = 0 )(x + 2)(2x² + 3x + 4)
The quadratic will not factor so we have to use the
quadratic formula to find the other two roots, by
setting the quadratic equal to zero:
2x² + 3x + 4 = 0




 So the roots are
So the roots are
 , -2, , -2, 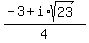 , , 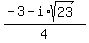 Are you allowed to use a TI-83 or TI-84 calculator on tests?
If so you can shorten your work by not having to try so many
numbers as candidates for rational roots.
Edwin
Are you allowed to use a TI-83 or TI-84 calculator on tests?
If so you can shorten your work by not having to try so many
numbers as candidates for rational roots.
Edwin
|
|
|