Question 331300: Factor the polynomial x^3+8x^2+19x+12
Answer by jrfrunner(365)   (Show Source): (Show Source):
You can put this solution on YOUR website! Factor the polynomial 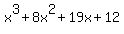
Since the highest degree is 3, there exist 3 roots to this poynomial
The real roots (there might be some complex roots) will be from the set
-/+1, -/+2, -/+3, -/+4,-/+6, -/+12
Use Discarte's sign rule
Number of positive roots P(x) ++++ no sign change, so no positive roots
number of negative roots P(-x) -+-+ 3 sign changes, so either 3 negative roots or 1 negative root and 2 complex roots
Since we know that at least one of the roots is negative, the roots are from
the set -1,-2,-3,-4,-6,-12
so experiment with -1 and see  so -1 is a root. so -1 is a root.
Now apply either long division or synthetic division to reduce the polynomial by one degree yield 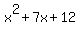 this can be easily factored into (x+3)(x+4) this can be easily factored into (x+3)(x+4)
so the original polymial can be factord into

|
|
|