SOLUTION: Factor completely. 49a^2+4-28a

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Factor completely. 49a^2+4-28a      Log On


   

Question 330746: Factor completely. 49a^2+4-28a
Answer by neatmath(302) About Me  (Show Source):
You can put this solution on YOUR website!

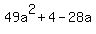
49a%5E2%2B4-28a

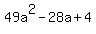
49a%5E2-28a%2B4

We must use the factors of the first term to see how this can be factored, using either 49 and 1, or 7 and 7.

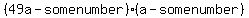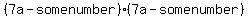
%2849a-somenumber%29%28a-somenumber%29 or %287a-somenumber%29%287a-somenumber%29

Notice that both factors must have a negative sign in them, since the last term is positive, but the middle term is negative.

Then we just have to use the factors of 4 to see what numbers will work to factor this.

This is just a matter of guessing and checking, or trial and error. Factors of 4 are 4 and 1, or 2 and 2. So our answer MUST be one of the following, if this polynomial is factorable:

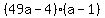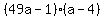%2849a-4%29%28a-1%29 or %2849a-1%29%28a-4%29 or %2849a-2%29%2849a-2%29 or

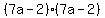
%287a-4%29%287a-1%29 or %287a-2%29%287a-2%29

Upon closer inspection, we can see that:

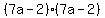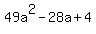
%287a-2%29%287a-2%29 does indeed multiply out to 49a%5E2-28a%2B4

so the answer is 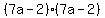%287a-2%29%287a-2%29

This polynomial is a special one, in the form of:

a%5E2-2ab%2Bb%5E2=%28a-b%29%5E2

where a=7a and b=2

Factoring polynomials is hard, and it takes a lot of practice. There are also different ways to approach this problem, but I hope this helps!