Tomas can do a job in 4 hours. Julia can do the same job in 6 hours.
Heres the way to do it quickly in your head. Then we'll do it by algebra,
the way your teacher wants you to do it. But for fun. let's do it the
easy way first:
The least common multiple of 4 hours and 6 hours is 12 hours. If they worked
together for 12 hours Thomas would do 3 jobs and Julia would do 2 jobs. So
together it would take them 12 hours to do 5 jobs or  ths
hours to do one job, which is
ths
hours to do one job, which is 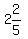 ths or 2.4 hours.
By algebra, make this chart:
Number of jobs Time in hours Rate in jobs/hour
Tomas
Julia
Both together
Let the time for both together be x. and the times for each are
given so fill in all three times:
Number of jobs Time in hours Rate in jobs/hour
Tomas 4
Julia 6
Both together x
We are interested in how long it take each and both to do just 1 job,
so we fill in the number of jobs as 1 in each case:
Number of jobs Time in hours Rate in jobs/hour
Tomas 1 4
Julia 1 6
Both together 1 x
Next use
ths or 2.4 hours.
By algebra, make this chart:
Number of jobs Time in hours Rate in jobs/hour
Tomas
Julia
Both together
Let the time for both together be x. and the times for each are
given so fill in all three times:
Number of jobs Time in hours Rate in jobs/hour
Tomas 4
Julia 6
Both together x
We are interested in how long it take each and both to do just 1 job,
so we fill in the number of jobs as 1 in each case:
Number of jobs Time in hours Rate in jobs/hour
Tomas 1 4
Julia 1 6
Both together 1 x
Next use  to fill in the three
rates:
Number of jobs Time in hours Rate in jobs/hour
Tomas 1 4 1/4
Julia 1 6 1/6
Both together 1 x 1/x
To get the equation, use
Tomas' rate + Julia's rate = their rate together
1/4 + 1/6 = 1/x
to fill in the three
rates:
Number of jobs Time in hours Rate in jobs/hour
Tomas 1 4 1/4
Julia 1 6 1/6
Both together 1 x 1/x
To get the equation, use
Tomas' rate + Julia's rate = their rate together
1/4 + 1/6 = 1/x
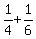

 Multiply through by LCD 12x
Multiply through by LCD 12x
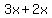







 hours.
Edwin
hours.
Edwin