Question 307270: If (y -3)^2 = 16, what is the smallest possible value of y^2?
Found 3 solutions by Theo, MathTherapy, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! (y-3)^2 = 16
Take square root of both sides of the equation to get:
y-3 = 4
Add 3 to both sides of the equation to get:
y = 7
The only value that y can be is 7.
There is no other value of y that would satisfy this equation which is why I wonder why you asked for the smallest value of y.
Substitute for 7 in the original equation to get:
(7-3)^2 = 16 which becomes:
4^2 = 16 which becomes:
16 = 16 which is true, confirming that y = 7 is the correct value to satisfy the equation.
If this was an inequality, such as:
(y-3)^2 >= 16, then you might ask for the smallest value of y.
You would solve the inequality pretty much the way you would solve the equality.
Take the square root of both sides of this equation to get:
y-3 >= 4
Add 3 to both sides of this equation to get:
y >= 7
The smallest value y could be then would be 7.
If you had the inequality equation of:
(y-3)^2 > 16, then you would solve again using the same method.
Take the square root of both sides of the equation to getr:
y-3 > 4
Add 3 to both sides of the equation to get y > 7
then the smallest value that y could be would be something greater than 7.
If you were looking for integers, it would be 8.
If you allowed real numbers than it could be anything as long as it was grater than 7.
7.01, 7.001, 7.0001, 7.000001, etc.
Answer by MathTherapy(10719)   (Show Source): (Show Source):
Answer by ikleyn(53614)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If (y -3)^2 = 16, what is the smallest possible value of y^2?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @Theo, giving the answer y = 7, is FATALLY incorrect.
I came to bring a correct solution.
If (y-3)^2 = 16, then there are two cases.
(1) Either y-3 = 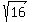 = 4, and then y-3 = 4, giving y = 4+3 = 7, y^2 = 49;
(2) Or y-3 = = 4, and then y-3 = 4, giving y = 4+3 = 7, y^2 = 49;
(2) Or y-3 =  = -4, and then y-3 = -4, giving y = -4 + 3 = -1, y^2 = (-1)^2 = 1.
y^2 = 1 is less than y^2 = 49. Therefore, the answer to the problem is THIS:
+---------------------------------------------+
| The smallest possible value of y^2 is 1. |
+---------------------------------------------+ = -4, and then y-3 = -4, giving y = -4 + 3 = -1, y^2 = (-1)^2 = 1.
y^2 = 1 is less than y^2 = 49. Therefore, the answer to the problem is THIS:
+---------------------------------------------+
| The smallest possible value of y^2 is 1. |
+---------------------------------------------+
Solved correctly, in a way as it SHOULD be done.
This problem is partly a Math joke, partly a Math trap, and partly a test
to check if a person does understand what is square root of a number.
|
|
|