Question 302370: an athlete whose event is the shot put releases a shot. when the shot is released at an angle of 35 degree, its height, f(x), in feet, can be modeled by f(x)=-0.01x2+0.7x+5.3, where x is the shot's horizontal ditance, in feet, from its point of release.
a. what is the maximum height of the shot and how far from its point of release does this occur?
the maximum height is ____, which occurs ____feet from the point of release.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! an athlete whose event is the shot put releases a shot.
when the shot is released at an angle of 35 degree, its height, f(x), in feet,
can be modeled by f(x)=-0.01x2+0.7x+5.3, where x is the shot's horizontal
distance, in feet, from its point of release.
:
a. what is the maximum height of the shot and how far from its point of release does this occur?
the maximum height is ____, which occurs ____feet from the point of release.
:
f(x)=-0.01x^2 +0.7x + 5.3
Find the axis of symmetry using the formula: x = -b/(2a)
where: a=-.01, b=.7
:
x = 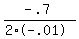
x = 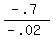
x = 35 ft, the horizontal dist to find max height
:
Find the height, replace x with 35 in the original equation
h = =-0.01(35^2) +0.7(35) + 5.3
h = -.01*1225 + 24.5 + 5.3
h = -12.25 + 24.5 + 5.3
h = 17.55 ft is the max height
|
|
|