SOLUTION: i am haveing trouble factoring this. can you please help me? {{{21x^5-24x^2-6x^4}}}

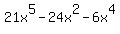
First we rearrange the terms in descending order of
exponents of x, by swapping the 2nd and 3rd terms:



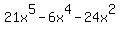We first look at 21, 6, and 24, and realize that the
largest integer that divides into all of them is 3,
and so that is the largest integer that can be
factored out

Then we look at the 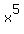,  and 
and realize that the LARGEST exponent of x which can
be factored out is the SMALLEST one that occurs in any
term.  That is, 

So we factor out 

so we write this followed by an opening parenthesis:



We divide 3 into 21 and get 7, and write this next:



Then we divide  into 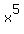 by subtracting exponents,
getting , write that next to the 7 and we have this so far:



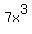Now we look at second term of the original which is 

We divide 3 into -6 and get -2, and write this next:



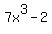Then we divide  into  by subtracting exponents,
getting , write that next to the 2 and we have this so far:



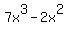Now we look at last term of the original which is 

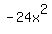We divide 3 into -24 and get -8, and write this next:



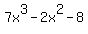Then we divide  into , and since they are the
same, we just get 1, and we don't have to write anything, and
since this is the last term we have finished factoring, so we
write a closing parenthesis, and we are done:



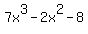
Edwin