|
Question 29084: i need help on the approach to solve the problem: the number eggs N in a female moth is a function of her abdominal width W, in millimeters, modeled by
N=14W^3 - 17W^2 - 16W + 34 , for 1.5 < W < 3.5
what is the abdominal width when there are 211 eggs?
Found 2 solutions by longjonsilver, venugopalramana:
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
When N=211, we get 

You have a cubic that needs to be solved. The method is either plot this on a graph and hope for integer solutions. Even so, you will still need to check algebraically.
So, start algebraically. We need to find one factor for this equation. This is trial and error, i'm afraid.
Lets try W=1 --> this will not give you zero. Check it
Lets try W=-1 --> this won't either
Lets try W=2 --> 14(2)^3 - 17(2)^2 - 16(2) - 177
----> 14(8) - 17(4) - 16(2) - 177
----> 112 - 68 - 32 - 177
--> not zero...
Lets try W=-2 --> 14(-2)^3 - 17(-2)^2 - 16(-2) - 177
----> 14(-8) - 17(4) - 16(-2) - 177
----> -112 - 68 + 32 - 177
--> not zero
Lets try W=3 --> 14(3)^3 - 17(3)^2 - 16(3) - 177
14(27) - 17(9) - 16(3) - 177
378 - 153 - 48 - 177
--> this is zero
So, W=3 is a solution, and (W-3) is therefore a factor.
Looking at the question, W=3 is within the bounds set, so this is an answer... there may well be more though. To find the other solutions, we need to find the other factor and solve that part of the equation.
So, we now need to divide  by (W-3) to find the other factor. This is long division...i cannot write it down here, but you will have done this before, since you have been asked this question. by (W-3) to find the other factor. This is long division...i cannot write it down here, but you will have done this before, since you have been asked this question.
You get 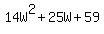 as the other factor. And where does this equal zero? ie as the other factor. And where does this equal zero? ie  ? Looking at the discriminant of this --> ? Looking at the discriminant of this --> 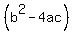 , this is negative, so there are no other "real" solutions... the cubic ONLY crosses the x-axis (y=0) once, at W=3. , this is negative, so there are no other "real" solutions... the cubic ONLY crosses the x-axis (y=0) once, at W=3.
jon.
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! i need help on the approach to solve the problem: the number eggs N in a female moth is a function of her abdominal width W, in millimeters, modeled by
N=14W^3 - 17W^2 - 16W + 34 , for 1.5 < W < 3.5
what is the abdominal width when there are 211 eggs?
THAT IS WE HAVE TO FIND W SO THAT N BECOMES EQUAL TO 211.
N=14W^3 - 17W^2 - 16W + 34 =211
for 1.5 < W < 3.5
14W^3 - 17W^2 - 16W + 34 - 211 =0
14W^3 - 17W^2 - 16W - 177 =0
14W^3 = 17W^2 + 16W + 177 .........I
SINCE 1.5 < W < 3.5,W IS POSITIVE..SO WE HAVE TO SEE THAT FOR POSITIVE W IN THE RANGE 1.5 < W < 3.5,L.H.S. = R.H.S.WE FIND THAT FOR POSITIVE W BOTH SIDES ARE POSITIVE AND FURTHER ALL TERMS ON R.H.S. ARE POSITIVE.SO WE TRY INTEGRAL VALUES FROM W =1 TO 2 TO 3 FIRST AND PROBE FOR INTEGRAL SOLUTION.SO WE GET
W......................................1.........2...........3............
L.H.S.=14W^3=..........................14........112.........378..........
R.H.S.=17W^2 + 16W + 177 =.............210.......278.........378...........
SO W =3 MM
NOTE THAT THIS IS THE STANDARD TRIAL AND ERROR APPROACH TO SOLVING THIRD OR HIGHHER DEGREE EQUATIONS.IF WE FAIL IN GETTING AN INTEGRAL VALUE,WE WILL ATLEAST KNOW THAT IT LIES BETWEEN 2 INTEGERS BY SEEING THAT AT ONE VALUE RHS>LHS ANMD AT THE NEXT VALUE LHS>RHS OR VICE VERSA..WHICH TELLS US THAT THE ANSWER IS BETWEEN THOSE 2 INTEGERS.HERE AS W INCREASES , WE FIND LHS IS CATCHING UP WITH RHS.WE GOT AN INTEGRAL ANSWER IN THIS CASE.
OTHER METHOD IS TO DRAW GRAPH OF LHS AND RHS IN ONE SHEET AND SEE WHERE THEY INTERSECT...SEE BELOW...FOR GRAPHICAL METHOD...

WE FIND THAT THE 2 CURVES MEET AT X=3 OR W=3..IS THE SOLUTION.
|
|
|
| |