How do i factor 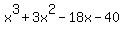
Since the leading coefficient is 1, if there
are any rational zeros, they will all be
± the integer factor of the absolute value of the
numerical term -40. So if there are any, they will
be among these:
±1,±2,±4,±5,±8,±10,±20
We begin by trying +1 using synthetic division:
1 | 1 3 -18 -40
| 1 4 -14
1 4 -14 -54
So, 1 is not a zero, and so x-1 is not a factor.
We try -1:
-1 | 1 3 -18 -40
| -1 -2 20
1 2 -20 -20
So, -1 is not a zero, and so x+1 is not a factor.
We try +2:
2 | 1 3 -18 -40
| 2 10 -16
1 5 -8 -56
So, 2 is not a zero, and so x-2 is not a factor.
We try -2:
-2 | 1 3 -18 -40
| -2 -2 40
1 1 -20 0
Eureka! We get a 0 remainder, so x+2 is a factor.
An the numbers on the bottom row of the synthetic
division left of the remainder 0 tell us the other
factor. So we have now factored
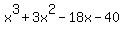 as
as
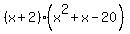 Now we can factor the trinomial in
the second parentheses and we have the
complete factorization as:
Now we can factor the trinomial in
the second parentheses and we have the
complete factorization as:
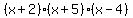 Edwin
Edwin