|
Question 204503:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
 Start with the given function Start with the given function
 Replace each "x" with "x+h" Replace each "x" with "x+h"
 FOIL (ie expand) FOIL (ie expand)
--------------------------------
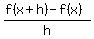 Move onto the given difference quotient. Move onto the given difference quotient.
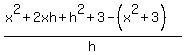 Plug in Plug in  and and 
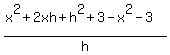 Distribute Distribute
 Combine like terms. Combine like terms.
 Factor out the GCF "h" from the numerator. Factor out the GCF "h" from the numerator.
 Cancel out the common terms. Cancel out the common terms.
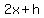 Simplify Simplify
So  when when 
=====================================================================================
# 2
Take note that when  it is less than zero. Because it is less than zero. Because  when when  , this means that we simply plug in , this means that we simply plug in  to get: to get:  . .
So 
Also, when  it is greater than zero. Since it is greater than zero. Since  when when  , we just plug in , we just plug in  to get: to get:  . .
So 
================================
# 3
 Start with the given equation. Start with the given equation.
 Add 3 to both sides. Add 3 to both sides.
 Subtract Subtract  from both sides. from both sides.
 Rearrange the terms. Rearrange the terms.
 Divide both sides by Divide both sides by  to isolate y. to isolate y.
 Break up the fraction and simplify. Break up the fraction and simplify.
We can see that the equation  has a slope has a slope  and a y-intercept and a y-intercept  . .
Now to find the slope of the perpendicular line, simply flip the slope  to get to get  . Now change the sign to get . Now change the sign to get  . So the perpendicular slope is . So the perpendicular slope is  . .
Now let's use the point slope formula to find the equation of the perpendicular line by plugging in the slope  and the coordinates of the given point and the coordinates of the given point ) . .
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Rewrite Rewrite 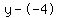 as as 
 Distribute Distribute
 Multiply Multiply
 Subtract 4 from both sides. Subtract 4 from both sides.
 Combine like terms. Combine like terms.
So the equation of the line perpendicular to  that goes through the point that goes through the point ) is is  . .
Here's a graph to visually verify our answer:

Graph of the original equation  (red) and the perpendicular line (red) and the perpendicular line  (green) through the point (green) through the point ) . .
=================================
# 5
 Start with the given equation Start with the given equation
 Group like terms. Group like terms.
 Take half of the x-coefficient -8 to get -4. Square -4 to get 16. Add this value to both sides. Take half of the x-coefficient -8 to get -4. Square -4 to get 16. Add this value to both sides.
 Take half of the y-coefficient -6 to get -3. Square -3 to get 9. Add this value to both sides. Take half of the y-coefficient -6 to get -3. Square -3 to get 9. Add this value to both sides.
 Combine like terms. Combine like terms.
 Rewrite 25 as Rewrite 25 as 
Now the equation is in the form  (which is a circle) where (h,k) is the center and "r" is the radius (which is a circle) where (h,k) is the center and "r" is the radius
In this case,  , ,  , and , and 
So the center is (4,3) and the radius is 5 units.
Here's the graph:

|
|
|
| |