Question 204273: Find the remainder when 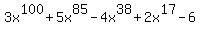 is divide by x+1 is divide by x+1
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is easy to divide a polynomial by (x+1), however with exponents of 100, it becomes tedious, as all exponents must be "filled in" to make algorithm work.
.
However, The REMAINDER THEOREM states," if a polynomial,f(x) is divided by
(x-k), the remainder is , r=f(k)"
.
given (x+1) = (x-k),,,k=(-1)
.
To find remainder, evaluate, f(-1), that is substitute (-1) for (x)
.
f(-1) = 3(-1)^100 +5(-1)^85 -4(-1)^38 +2(-1)^17 -6
.
f(-1) = +3(1)+5(-1)-4(1) +2(-1) -6
.
f(-1) = -14,,,,,and REMAINDER = (-14)
.
|
|
|