SOLUTION: (n^2+5n+6/n^2+7n+12)(n^2+9n+20/n^2+11n+30)= ?

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: (n^2+5n+6/n^2+7n+12)(n^2+9n+20/n^2+11n+30)= ?      Log On


   

Question 203065: (n^2+5n+6/n^2+7n+12)(n^2+9n+20/n^2+11n+30)= ?
Found 3 solutions by Earlsdon, jim_thompson5910, jsmallt9:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!

Factor the trinomials in the numerators and the denominators.
Now cancel the common factors as shown to leave you with:
highlight%28%28n%2B2%29%2F%28n%2B6%29%29

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

Start with the given expression.


Factor n%5E2%2B5n%2B6 to get %28n%2B3%29%28n%2B2%29.


Factor n%5E2%2B7n%2B12 to get %28n%2B4%29%28n%2B3%29.


Factor n%5E2%2B9n%2B20 to get %28n%2B5%29%28n%2B4%29.


Factor n%5E2%2B11n%2B30 to get %28n%2B6%29%28n%2B5%29.


Combine the fractions.


Highlight the common terms.


Cancel out the common terms.


%28n%2B2%29%2F%28n%2B6%29 Simplify.


So simplifies to %28n%2B2%29%2F%28n%2B6%29.


In other words,

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!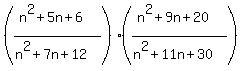

This is not an equation. It is an expression. And all you can do with expressions is to simplify them. Simplifying includes (but is not limited to):
  1. Reduce fractions
  2. Go through the order of operations (aka PEMDAS) to perform any possible operations

How do you reduce fractions? When there are just numbers involved (i.e. no variables) we usually
  1. Go through PEMDAS in the numerator and in the denominator so that each is just a single number
  2. Look for numbers which will divide evenly into both the numerator and the denominator. If we find a number, other than 1, that will divide evenly then we divide both the numerator and denominator by that number.
  3. Repeat step 2 until the only number that divides evenly is 1.

What we often forget about the above procedure is that we what we are really doing is canceling common factors. We express the numerator and denominator as a product of some factors. And if there are common factors in the numerator and denominator we can cancel them out. Understanding this is the key to reducing the fractions in expressions like your: Factor the numerators and denominators and see if there are common factors to cancel.
To factor:
  1. Always start by factoring out the Greatest Common Factor (GCF), if it is not 1.
    In your fractions the GCF of all the numerators and denominators is 1 so we can't do anything useful. (But it is important to check for a GCF first!.)
  2. Try any and all of the following techniques (most of which you should have heard of by now):
    • Factor by patterns:
      • Difference of squares: a%5E2+-+b%5E2+=+%28a+%2B+b%29%28a+-+b%29
      • Difference of Cubes: a%5E3+-+b%5E3+=+%28a+-+b%29%28a%5E2+%2B+ab+%2B+b%5E2%29
      • Sum of Cubes: a%5E3+%2B+b%5E3+=+%28a+%2B+b%29%28a%5E2+-+ab+%2B+b%5E2%29

        • Note: There is no "Sum of Squares" pattern. These are called patterns because, for example, the "Difference of Squares" pattern can be used to factor any two-term expression which is a difference of two perfect squares. These can be a little hard to see until you get practice. 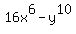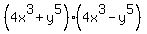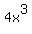For example, 16x%5E6+-+y%5E10 is a difference of squares: %284x%5E3%29%5E2+-+%28y%5E5%29%5E2%29 and so it will factor, according to the pattern into %284x%5E3+%2B+y%5E5%29%284x%5E3+-+y%5E5%29 (using 4x%5E3 as "a" and y%5E5 as "b".
    • Factoring trinomials (three term expressions) of the form: ax%5E2+%2B+bx+%2B+c. There are two cases determined by the value of "a" (the coefficient of the prefect square at the front of the expression):
      1. a = 1: This is the easiest (which is fortunate since all of your numerators and denominators are in this form.) The key to factoring these is the answer to the following question: "What are the factors of 'c' (the number at the end) which add up to 'b' (the coefficient of the middle term)? Remember that if "c" is positive there are two negative factors which may be the answer to the question.
      2. a is not 1. These are much harder and, since we will not need this for your problem, I will skip trying to explaining it. here.
    • Factoring by Grouping. Since we will not need this for your problem, I will skip trying to explaining it.
    • Factoring by trial and error using the possible rational roots. Since we will not need this for your problem, I will skip trying to explaining it.
  3. Repeat using any and all of the above until you cannot factor any further

As already mentioned, all your numerators and denominators:
  • Have a GCF which is 1 (which we don't bother factoring out).
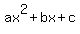  • Are trinomials of the for ax%5E2+%2B+bx+%2B+c+ with a = 1

So we start by asking the question "What factors of 'c' add up to 'b'?
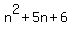n%5E2%2B5n%2B6 What factors of 6 add up to 5? Answer: 2 and 3. So n%5E2%2B5n%2B6+=+%28x+%2B+2%29%28x+%2B+3%29
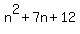n%5E2%2B7n%2B12 What factors of 12 add up to 7? Answer: 3 and 4. So n%5E2%2B7n%2B12+=+%28x+%2B+3%29%28x+%2B+4%29
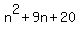n%5E2%2B9n%2B20 What factors of 20 add up to 9? Answer: 4 and 5. So n%5E2%2B9n%2B20+=+%28x+%2B+4%29%28x+%2B+5%29
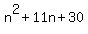n%5E2%2B11n%2B30 What factors of 30 add up to 11? Answer: 5 and 6. So n%5E2%2B11n%2B30+=+%28x+%2B+5%29%28x+%2B+6%29
Replacing each of these numerators and denominators with their factored form we get

Now we will cancel common factors. And since we are multiplying fractions we are allowed to "cross cancel" (cancel common factors even if they are in differnent fractions).

After multiplying what is left we end up with the reduced fraction:
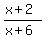
%28x+%2B+2%29%2F%28x+%2B+6%29
There is no further simplifying which can be done so this is the answer.