SOLUTION: Hello! Find all real zeros of the polynomial. Use the quadratic formula if necessary P(x) = x^4 + x^3 - 5x^2 - 4x + 4 thanks for your help!

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Hello! Find all real zeros of the polynomial. Use the quadratic formula if necessary P(x) = x^4 + x^3 - 5x^2 - 4x + 4 thanks for your help!      Log On


   

Question 199774: Hello!
Find all real zeros of the polynomial. Use the quadratic formula if necessary
P(x) = x^4 + x^3 - 5x^2 - 4x + 4
thanks for your help!
Found 2 solutions by jim_thompson5910, Alan3354:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
First, let's find the possible rational zeros of P(x):

Any rational zero can be found through this equation

where p and q are the factors of the last and first coefficients


So let's list the factors of 4 (the last coefficient):



Now let's list the factors of 1 (the first coefficient):



Now let's divide each factor of the last coefficient by each factor of the first coefficient









Now simplify

These are all the distinct rational zeros of the function that could occur



----------------------------------------------------------------------------------------

Now let's see which possible roots are actually roots.


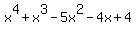
Let's see if the possible zero 1 is really a root for the function x%5E4%2Bx%5E3-5x%5E2-4x%2B4


So let's make the synthetic division table for the function 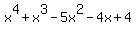x%5E4%2Bx%5E3-5x%5E2-4x%2B4 given the possible zero 1:
1|11-5-44
| 12-3-7
12-3-7-3

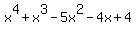
Since the remainder -3 (the right most entry in the last row) is not equal to zero, this means that 1 is not a zero of x%5E4%2Bx%5E3-5x%5E2-4x%2B4


------------------------------------------------------


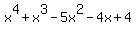
Let's see if the possible zero 2 is really a root for the function x%5E4%2Bx%5E3-5x%5E2-4x%2B4


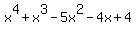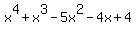
So let's make the synthetic division table for the function x%5E4%2Bx%5E3-5x%5E2-4x%2B4 given the possible zero 2:
2|11-5-44
| 262-4
131-20

Since the remainder 0 (the right most entry in the last row) is equal to zero, this means that 2 is a zero of x%5E4%2Bx%5E3-5x%5E2-4x%2B4


So this means that x%5E4%2Bx%5E3-5x%5E2-4x%2B4=%28x-2%29%28x%5E3%2B3x%5E2%2Bx-2%29


Note: the term x%5E3%2B3x%5E2%2Bx-2 was formed by the first four values in the bottom row.


Now that you have x%5E3%2B3x%5E2%2Bx-2, you simply find the possible rational zeros for x%5E3%2B3x%5E2%2Bx-2 and test to see which ones are really zeros (ie repeat the first two steps).

It turns out that the possible roots for x%5E3%2B3x%5E2%2Bx-2 are: 1, 2, -1, -2

and that -2 is a root of x%5E3%2B3x%5E2%2Bx-2

Here's the synthetic division to prove it:

-2|131-2
| -2-22
11-10


Looking at the bottom row of values (everything but the remainder), we get 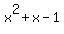x%5E2%2Bx-1. So this means that

x%5E3%2B3x%5E2%2Bx-2=%28x%2B2%29%28x%5E2%2Bx-1%29


Note: this consequently means that x%5E4%2Bx%5E3-5x%5E2-4x%2B4=%28x-2%29%28x%2B2%29%28x%5E2%2Bx-1%29


Now we just need to solve x%5E2%2Bx-1=0 to find the last remaining zeros.



x%5E2%2Bx-1=0 Start with the given equation.


Notice we have a quadratic in the form of Ax%5E2%2BBx%2BC where A=1, B=1, and C=-1


Let's use the quadratic formula to solve for "x":


x+=+%28-B+%2B-+sqrt%28+B%5E2-4AC+%29%29%2F%282A%29 Start with the quadratic formula


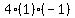x+=+%28-%281%29+%2B-+sqrt%28+%281%29%5E2-4%281%29%28-1%29+%29%29%2F%282%281%29%29 Plug in A=1, B=1, and C=-1


x+=+%28-1+%2B-+sqrt%28+1-4%281%29%28-1%29+%29%29%2F%282%281%29%29 Square 1 to get 1.


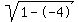x+=+%28-1+%2B-+sqrt%28+1--4+%29%29%2F%282%281%29%29 Multiply 4%281%29%28-1%29 to get -4


x+=+%28-1+%2B-+sqrt%28+1%2B4+%29%29%2F%282%281%29%29 Rewrite sqrt%281--4%29 as sqrt%281%2B4%29


x+=+%28-1+%2B-+sqrt%28+5+%29%29%2F%282%281%29%29 Add 1 to 4 to get 5


x+=+%28-1+%2B-+sqrt%28+5+%29%29%2F%282%29 Multiply 2 and 1 to get 2.


x+=+%28-1%2Bsqrt%285%29%29%2F%282%29 or x+=+%28-1-sqrt%285%29%29%2F%282%29 Break up the expression.


So the last two roots are x+=+%28-1%2Bsqrt%285%29%29%2F%282%29 or x+=+%28-1-sqrt%285%29%29%2F%282%29


====================================================================================

Answer:


So the four zeros of P%28x%29+=+x%5E4+%2B+x%5E3+-+5x%5E2+-+4x+%2B+4+are:

x=2, x=-2, x+=+%28-1%2Bsqrt%285%29%29%2F%282%29 or x+=+%28-1-sqrt%285%29%29%2F%282%29


Note: if you wanted to, you could compactly write the zeros as:

x=%22%22%2B-+2, x+=+%28-1%2B-sqrt%285%29%29%2F%282%29

just remember that there are 4 zeros.



If you have any questions, email me at jim_thompson5910@hotmail.com.
Check out my website if you are interested in tutoring.

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Find all real zeros of the polynomial. Use the quadratic formula if necessary
P(x) = x^4 + x^3 - 5x^2 - 4x + 4
--------------
By graphing, x = 2 and x = -2
-------------------
Divide by (x^2 - 4) to get:
x^2 + x - 1 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B1x%2B-1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%281%29%5E2-4%2A1%2A-1=5.

Discriminant d=5 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-1%2B-sqrt%28+5+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%281%29%2Bsqrt%28+5+%29%29%2F2%5C1+=+0.618033988749895
x%5B2%5D+=+%28-%281%29-sqrt%28+5+%29%29%2F2%5C1+=+-1.61803398874989

Quadratic expression 1x%5E2%2B1x%2B-1 can be factored:
1x%5E2%2B1x%2B-1+=+%28x-0.618033988749895%29%2A%28x--1.61803398874989%29
Again, the answer is: 0.618033988749895, -1.61803398874989. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B1%2Ax%2B-1+%29

---------------
I got the +2 and -2 by graphing using the software from
www.padowan.dk.com/graph/
FREE software, btw