SOLUTION: please help me with these two problems {{{x^3+64=0}}} this is how far i got x^3+64=x+21.3 =(x+21.3)((x^2)-x+21.3) =(x+21.3)(x^2-x+21.3) and i have one more problem {{{

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: please help me with these two problems {{{x^3+64=0}}} this is how far i got x^3+64=x+21.3 =(x+21.3)((x^2)-x+21.3) =(x+21.3)(x^2-x+21.3) and i have one more problem {{{      Log On


   

Question 185416This question is from textbook prentice hall mathematics algebra 2
: please help me with these two problems
x%5E3%2B64=0
this is how far i got
x^3+64=x+21.3
=(x+21.3)((x^2)-x+21.3)
=(x+21.3)(x^2-x+21.3)
and i have one more problem
x%5E3-125=0 This question is from textbook prentice hall mathematics algebra 2

Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
1) Solve:
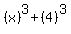x%5E3%2B64+=+0 This is the sum of two cubes: %28x%29%5E3%2B%284%29%5E3 and this is factorable as:
A%5E3%2BB%5E3+=+%28A%2BB%29%28A%5E2-AB%2BB%5E2%29 and in your problem, A = x and B = 4,so...
x%5E3%2B64+=+%28x%2B4%29%28x%5E2-4x%2B16%29, so...
%28x%2B4%29%28x%5E2-4x%2B16%29+=+0 Applying the zero product rule, we get:
x%2B4+=+0 or x%5E2-4x%2B16++=0
If x%2B4+=+0 then highlight%28x+=+-4%29 and...
If x%5E2-4x%2B16+=+0 Use the quadratic formula (x+=+%28-b%2B-sqrt%28b%5E2-4ac%29%29%2F2a) to solve:
x+=+%28-%28-4%29%2B-sqrt%28%28-4%29%5E2-4%281%29%2816%29%29%29%2F2%281%29
x+=+%284%2B-sqrt%2816-64%29%29%2F2
x+=+%284%2B-sqrt%28-48%29%29%2F2 Simplifying this, we get:
x+=+%284%2B-sqrt%2816%2A%28-3%29%29%29%2F2
x+=+2%2B2%2Asqrt%28-3%29 or x+=+2-2sqrt%28-3%29 or these can be written in terms of i+=+sqrt%28-1%29
highlight%28x+=+2%2B2sqrt%283%29i%29} or highlight%28x+=+2-2sqrt%283%29i%29
So the three roots (there are three because it's a cubic equation) are:
highlight%28x+=+-4%29
highlight%28x+=+2%2B2sqrt%283%29i%29
highlight%28x+=+2-2sqrt%283%29i%29
-------------------------------------------------------------------
2) Solve:
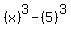x%5E3-125+=+0 This is the difference of two cubes (%28x%29%5E3-%285%29%5E3) and this is factorable as: A%5E3-B%5E3+=+%28A-B%29%28A%5E2%2BAB%2BB%5E2%29 and in this problem, A = x and B = 5, so...
x%5E3-125+=+%28x-5%29%28x%5E2%2B5x%2B25%29 so...
%28x-5%29%28x%5E2%2B5x%2B25%29+=+0 Again, applying the zero product rule, we get:
x-5+=+0 or x%5E2%2B5%2B25+=+0 so...
If x-5+=+0 then highlight%28x+=+5%29 or
If x%5E2%2B5x%2B25+=+0 Use the quadratic formula to solve:
x+=+%28-5%2B-sqrt%285%5E2-4%281%29%2825%29%29%29%2F2%281%29 Simplifying, we get:
x+=+%28-5%2B-sqrt%28-75%29%29%2F2
x+=+%28-5%2B-sqrt%2825%2A%28-3%29%29%29%2F2
x+=+%28-5%2F2%29%2B%285%2F2%29sqrt%28-3%29 or x+=+%28-5%2F2%29-%285%2F2%29sqrt%28-3%29%29 which can be written as:
highlight%28x+=+%28-5%2F2%29%281-sqrt%283%29i%29%29 or highlight%28x+=+%28-5%2F2%29%281%2Bsqrt%283%29i%29%29
So the three roots are:
highlight%28x+=+5%29
highlight%28x+=+%28-5%2F2%29%281-sqrt%283%29i%29%29
highlight%28x+=+%28-5%2F2%29%281%2Bsqrt%283%29i%29%29