Question 184808This question is from textbook Algebra and Trigonometry Structure and Method book 2
: I have been working on this math problem and I can't seem to figure it out. I was wondering if someone could help me? Please and Thank You!! I would deeply appreciate it!!
Find all intercepts of the parabola y-2=-1/2(x-4)^2
This question is from textbook Algebra and Trigonometry Structure and Method book 2
Found 2 solutions by jojo14344, MathTherapy:
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given:  ---> ---> , distribute , distribute  and transfer and transfer  to the right. to the right.

 , EQN 1 , EQN 1
First, we'll find the vertex thru Vertex form: 
where of the vertex of the vertex
we complete the square:
Divide the whole eqn by  : :
 ---> --->






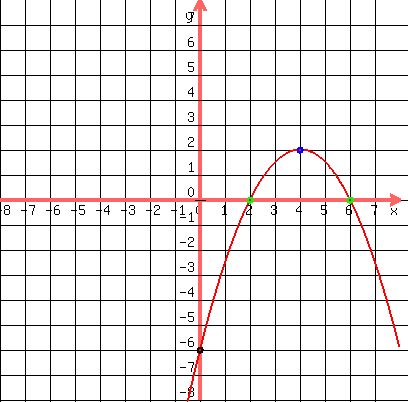
You see,  & &  --->VERTEX (4,2) --->VERTEX (4,2)
Next:
Let  , as per EQN 1 , as per EQN 1

 , Y Intercept , Y Intercept
Next:
For the X Intercepts, we solve the Eqn1:
by QUADRATIC, where
Solving for he discriminant: 
Therefore,


Also, 
Then we see the graph, plotting all intercepts:
Thank you,
Jojo
Answer by MathTherapy(10585)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I have been working on this math problem and I can't seem to figure it out. I was wondering if someone could help me?
Please and Thank You!! I would deeply appreciate it!!
Find all intercepts of the parabola y-2=-1/2(x-4)^2
TOTALLY, TOTALLY UNNECESSARY steps by the person who responded.

 ----- Adding 2 to both sides ----- Adding 2 to both sides
 ----- Vertex form of a parabola, where the VERTEX, (h, k) = (4, 2)
"h" is the x-coordinate of the vertex of the parabola, is also the paeabola's Axis of Symmetry, as well as the MIDWAY point
between the x-intercepts.
If MiDWAY between 2 points of a HORIZONTAL line is 4, then LEFT and RIGHT endpoints are: ----- Vertex form of a parabola, where the VERTEX, (h, k) = (4, 2)
"h" is the x-coordinate of the vertex of the parabola, is also the paeabola's Axis of Symmetry, as well as the MIDWAY point
between the x-intercepts.
If MiDWAY between 2 points of a HORIZONTAL line is 4, then LEFT and RIGHT endpoints are:  , and , and  .
Therefore, x-intercepts are 2 and 6, or at the coordinate points: (2, 0) and (6, 0).
Although more time-consuming, we can also do the following: .
Therefore, x-intercepts are 2 and 6, or at the coordinate points: (2, 0) and (6, 0).
Although more time-consuming, we can also do the following:

 ---- Adding 2 to both sides ---- Adding 2 to both sides

 ---- Substituting 0 for y, since y-values on x-axis are 0
- 2(0) = ---- Substituting 0 for y, since y-values on x-axis are 0
- 2(0) = 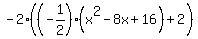 ---- Multiplying each side by - 2 ---- Multiplying each side by - 2
 (x - 2)(x - 6) = 0 ---- Factorizing the trinomial
x - 2 = 0 OR x - 6 = 0
x = 2 OR x = 6
x-INTERCEPTS: (2, 0) (6, 0)
(x - 2)(x - 6) = 0 ---- Factorizing the trinomial
x - 2 = 0 OR x - 6 = 0
x = 2 OR x = 6
x-INTERCEPTS: (2, 0) (6, 0)
|
|
|