SOLUTION: Without actual division prove that 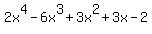{{{2x^4-6x^3+3x^2+3x-2}}} is exactly divisible by {{{x^2-3x+2}}}. How can we prove that without actual division? I tried to understand but it's t

.
First we factor  as 

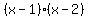So 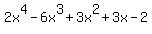 will be divisible by 
if and only if both  and 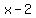 are both factors
of .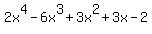

Now we know by the remainder theorem that if 
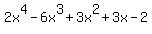 were to be divided by , 
the remainder would have the same value as 
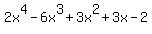 with x replaced by +1. 

Therefore the remainder of the division would be





.

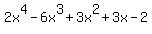
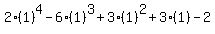
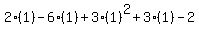
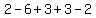
And since the remainder is 0, 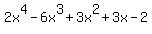 is
divisible by .  Now we do the same with the other
factor :

As before we know by the remainder theorem that if
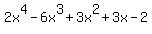 were to be divided by , the 
remainder would have the same value as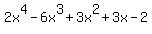 
with x replaced by +2. 

Therefore the remainder of the division would be





.

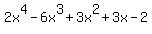
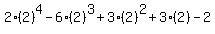
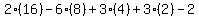
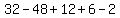
And since the remainder is 0, 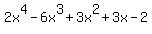 is
also divisible by .

And since 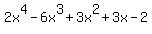 is divisible both
by  and  it is divisible by their
product 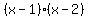 or , and we didn't
do any division!

Edwin