Can someone please help me with a couple of problems on polynomials finding the quotient and the remainder?
1) 
By long division you would start with
___________________
x - 3) 2x3 - 3x2 + x - 1
But with synthetic division
Change the sign of the -3 to +3
and write this:
3 |
|__________
Then list the coefficients of the terms:
3 |2 -3 1 -1
|__________
Start by bringing down the 2
3 |2 -3 1 -1
|__________
2
Multiply the 2 at the bottom by the 3 at the left,
getting 6. Write that 6 above and to the right of
the 2, under the next term -3:
3 |2 -3 1 -1
| 6
2
Combine the -3 and the 6, getting 3, and write this
below the line under the 6:
3 |2 -3 1 -1
| 6
2 3
Multiply that 3 on the bottom by the 3 at the left,
getting 9, and write this 9 above and to the right of the
3, above the line below the 1:
3 |2 -3 1 -1
| 6 9
2 3
Combine the 1 and the 9, getting 10, and write this
below the line under the 9:
3 |2 -3 1 -1
| 6 9
2 3 10
Multiply 10 on the bottom by the 3 at the left, getting 30,
and write this 30 above and to the right of the 10, above
the line below the -1:
3 |2 -3 1 -1
| 6 9 30
2 3 10
Combine the -1 and the 30, getting 29, and write this
29 below the line under the 30:
3 |2 -4 1 -1
| 6 9 30
2 3 10 29
Now we must interpret that row of numbers 2 3 10 29
across the bottom of the synthetic division.
The largest power of x in the original polynomial is 3.
So the 2 is multiplied by a power of x which is 1 lower
than the degree of the original polynomial. One lower
than 3 is 2, so we write x2 after the 2. Then we
write x (first power) after the 3. Then 10 is the
constant term. So the quotient only is
2x2 + 3x + 10
and the last number on the bottom right is the remainder. So
we put the remainder 29 over the divisor x - 3 and we have
as the final answer:
==========================================================
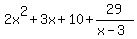2) 
d(x) = 
By long division you would start with
_____________________
x - 5) x3 - 9x2 + 15x + 25
But with synthetic division
Change the sign of the -5 to +5
and write this:
5 |
|__________
Then list the coefficients of the terms:
5 |1 -9 15 25
|__________
Start by bringing down the 1
5 |1 -9 15 25
|__________
1
Multiply the 1 at the bottom by the 5 at the left,
getting 5. Write that 5 above and to the right of
the 1, under the next term -9:
5 |1 -9 15 25
| 5
1
Combine the -9 and the 5, getting -4, and write this
below the line under the 5:
5 |1 -9 15 25
| 5
1 -4
Multiply that -4 on the bottom by the 5 at the left,
getting -20, and write this -20 above and to the right of the
-4, above the line below the 15:
5 |1 -9 15 25
| 5-20
1 -4
Combine the 15 and the -20, getting -5, and write this
below the line under the -20:
5 |1 -9 15 25
| 5-20
1 -4 -5
Multiply -5 on the bottom by the 5 at the left, getting -25,
and write this -25 above and to the right of the -5, above
the line below the -20:
5 |1 -9 15 25
| 5-20-25
1 -4 1-5
Combine the 25 and the -25, getting 0, and write this
0 below the line under the -25:
5 |1 -9 15 25
| 5-20-25
1 -4 -5 0
Now we must interpret that row of numbers 1 -4 -5 0
across the bottom of the synthetic division.
The largest power of x in the original polynomial is 3.
So the 1 is multiplied by a power of x which is 1 lower
than the degree of the original polynomial. One lower
than 3 is 2, so we write x2 after the 1. Then we
write x (first power) after the -4. Then -5 is the
constant term. So the quotient is
x2 - 4x - 5
and the last number on the bottom right is the remainder.
Since that number is 0, that is the final answer.
-----------------------------------------------------
3) P(x) = x4 + 6x3
d(x) = x-1
Nere we must use placeholders for x2, x1, and the constant
term
By long division you would start with
_______________________
x - 1) x4 + 6x3 + 0x + 0 + 0
But with synthetic division
Change the sign of the -1 to +1
and write this:
1 | 1 6 0 0 0
|__________________
Start by bringing down the 1
1 | 1 6 0 0 0
|__________________
1
Multiply the 1 at the bottom by the 1 at the left,
getting 1. Write that 1 above and to the right of
the 1 at the bottom, under the next term 6:
1 | 1 6 0 0 0
|_____1____________
1
Combine the 6 and the 1, getting 7, and write this
7 below the line under the 1:
1 | 1 6 0 0 0
|_____1____________
1 7
Multiply the 7 at the bottom by the 1 at the left,
getting 7. Write that 7 above and to the right of
the 7 at the bottom, under the next term 0:
1 | 1 6 0 0 0
|_____1___7________
1 7
Combine the 0 and the 7, getting 7, and write this
7 below the line under the 7:
1 | 1 6 0 0 0
|_____1___7________
1 7 7
Multiply the second 7 at the bottom by the 1 at the
left, getting 7. Write that 7 above and to the right of
the second 7 at the bottom, under the next term 0:
1 | 1 6 0 0 0
|_____1___7___7____
1 7 7
Combine the 0 and the 7, getting 7, and write this
7 below the line under the 7:
1 | 1 6 0 0 0
|_____1___7___7____
1 7 7 7
Multiply the third 7 at the bottom by the 1 at the
left, getting 7. Write that 7 above and to the right of
the third 7 at the bottom, under the last term 0:
1 | 1 6 0 0 0
|_____1___7___7___7
1 7 7 7
Combine the 0 and the 7, getting 7, and write this
7 below the line under the 7:
1 | 1 6 0 0 0
|_____1___7___7___7
1 7 7 7 7
Now we must interpret that row of numbers 1 7 7 7 7
across the bottom of the synthetic division.
The largest power of x in the original polynomial is 4.
So the 1 is multiplied by a power of x which is 1 lower
than the degree of the original polynomial. One lower
than 4 is 3, so we write x3 after the 1. Then we
write x2 after the first 7. Then x after the second 7.
The third 7 on the bottom is the constant term. The
quotient only is
x³ + 7x² + 7x + 7
and the last number on the bottom right is the remainder. So
we put the remainder 7 over the divisor x - 1 and we have
as the final answer:
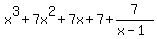Edwin
