Question 139361: rationalize the denominator of the fraction.3 sqrt 3 over 3 sqrt 7 i came up with 3 sqrt 147 over 7 but i have no idea if this is correct.thanks in advance for your help .also rewrite 5 sqrt c with a small 2 at the top of the c.for this one i got c 2/5
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Unless the number under the radical is a perfect square, like 4, 9, 16, 25..., then the square root is an irrational number. A rational number is one that can be expressed as the quotient of two integers,  where p and q are integers. An irrational number cannot be expressed this way. where p and q are integers. An irrational number cannot be expressed this way.
So rationalizing a denominator means 'get that nasty radical the heck out of my denominator'
In this problem, we need to multiply the denominator by  , so the denominator will become , so the denominator will become  . BUT, we have to do so in such a way that we don't change the value of the overall fraction. Since we know that anything multiplied by 1 is itself ( . BUT, we have to do so in such a way that we don't change the value of the overall fraction. Since we know that anything multiplied by 1 is itself ( no matter what a is), we can multiply the fraction by 1 in the form of no matter what a is), we can multiply the fraction by 1 in the form of  . ( . ( no matter what a is). no matter what a is).
But first a rule about radicals: No matter what a and b are (as long as they are positive) we can say that  . .
Now:
 . .
So we have a new fraction that is equivalent to the original, but has a rational number (21) in the denominator. Done.
For your other problem, I think you mean  . I'm a little concerned that you are referring to . I'm a little concerned that you are referring to  , meaning 'c squared' as "c with a small 2 at the top of the c" and you are in a class where you are being asked to rationalize denominators. The square root of something squared is just that thing, so , meaning 'c squared' as "c with a small 2 at the top of the c" and you are in a class where you are being asked to rationalize denominators. The square root of something squared is just that thing, so  , and your simplified expression is just , and your simplified expression is just 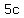 . But my concern is that your rather unsophisticated use of terminology indicates that you might have a significant gap in your grasp of algebraic fundamentals that can't be corrected by visiting help sites like this one. You should see your instructor and get him/her to provide you with some intensive remedial instruction. . But my concern is that your rather unsophisticated use of terminology indicates that you might have a significant gap in your grasp of algebraic fundamentals that can't be corrected by visiting help sites like this one. You should see your instructor and get him/her to provide you with some intensive remedial instruction.
|
|
|