SOLUTION: Please help me, I am lost. complete the square and write the equation in standard form. Then give the center and radius of the circle: x^2+y^2-2x-4y-4=0 Thank you so much

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Please help me, I am lost. complete the square and write the equation in standard form. Then give the center and radius of the circle: x^2+y^2-2x-4y-4=0 Thank you so much      Log On


   

Question 134905: Please help me, I am lost.
complete the square and write the equation in standard form. Then give the center and radius of the circle:
x^2+y^2-2x-4y-4=0
Thank you so much
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Step 1: Set the constant term on the right side of the equation:

x%5E2%2By%5E2-2x-4y=4

Step 2: Rearrange the terms, put the x terms together and the y terms together:

x%5E2-2x%2By%5E2-4y=4

Step 3: Divide the coefficient on the x term by 2, and then square the result:

%28%28-2%29%2F2%29%5E2=1

Step 4: Add this value to both sides of the equation:

x%5E2-2x%2B1%2By%5E2-4y=4%2B1

Step 5: Repeat steps 3 and 4 using the coefficient on the y term:

%28%28-4%29%2F2%29%5E2=4

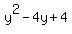x%5E2-2x%2B1%2By%5E2-4y%2B4=4%2B1%2B4

x%5E2-2x%2B1 is a perfect square, so x%5E2-2x%2B1=%28x-1%29%5E2

y%5E2-4y%2B4 is a perfect square, so y%5E2-4y%2B4=%28y-2%29%5E2

Step 6: Using this information, re-write the equation:

%28x-1%29%5E2%2B%28y-2%29%5E2=9

This is now in the standard form of an equation of a circle with center at (h,k) and radius r, namely %28x-h%29%5E2%2B%28y-k%29%5E2=r%5E2

Step 7: You can now tell by inspection that the x-coordinate of the center is 1, the y-coordinate of the center is 2, and the radius is sqrt%289%29=3.

C(1,2), r = 3