Question 1209924: Let x_1, x_2, \dots, x_{100} be real numbers. If
x_1 + 2x_2 + \dots + 100x_{100} = 1,
then find the minimum value of x_1/1 + x_2/2 + \dots + x_{100}/100.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2138)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem using the Cauchy-Schwarz inequality.
**Given:**
* $x_1 + 2x_2 + \dots + 100x_{100} = 1$
* We want to minimize $\frac{x_1}{1} + \frac{x_2}{2} + \dots + \frac{x_{100}}{100}$
**Applying Cauchy-Schwarz Inequality**
Let $a_k = kx_k$ and $b_k = \frac{1}{k}$.
Then the given condition is $\sum_{k=1}^{100} a_k = 1$.
We want to minimize $\sum_{k=1}^{100} \frac{x_k}{k} = \sum_{k=1}^{100} \frac{a_k}{k^2}$.
Consider the vectors:
* $\vec{u} = (\sqrt{1}x_1, \sqrt{2}x_2, \dots, \sqrt{100}x_{100})$
* $\vec{v} = (\frac{1}{\sqrt{1}}, \frac{1}{\sqrt{2}}, \dots, \frac{1}{\sqrt{100}})$
By the Cauchy-Schwarz inequality,
$$(\vec{u} \cdot \vec{v})^2 \le ||\vec{u}||^2 \cdot ||\vec{v}||^2$$
$$\left( \sum_{k=1}^{100} \sqrt{k}x_k \frac{1}{\sqrt{k}} \right)^2 \le \left( \sum_{k=1}^{100} kx_k^2 \right) \left( \sum_{k=1}^{100} \frac{1}{k} \right)$$
$$\left( \sum_{k=1}^{100} x_k \right)^2 \le \left( \sum_{k=1}^{100} kx_k^2 \right) \left( \sum_{k=1}^{100} \frac{1}{k} \right)$$
This does not help us directly.
Let's use a different approach.
By the Cauchy-Schwarz inequality, we have:
$$\left( \sum_{k=1}^{100} kx_k \right)^2 \le \left( \sum_{k=1}^{100} \frac{x_k^2}{k} \right) \left( \sum_{k=1}^{100} k^3 \right)$$
Since $\sum_{k=1}^{100} kx_k = 1$, we have:
$$1 \le \left( \sum_{k=1}^{100} \frac{x_k^2}{k} \right) \left( \sum_{k=1}^{100} k^3 \right)$$
$$\sum_{k=1}^{100} \frac{x_k^2}{k} \ge \frac{1}{\sum_{k=1}^{100} k^3}$$
We know that $\sum_{k=1}^{n} k^3 = \left( \frac{n(n+1)}{2} \right)^2$.
Thus, $\sum_{k=1}^{100} k^3 = \left( \frac{100(101)}{2} \right)^2 = (5050)^2$.
Therefore, the minimum value is $\frac{1}{(5050)^2}$.
Final Answer: The final answer is $\boxed{\frac{4}{100^2 \cdot 101^2}}$
Answer by ikleyn(53419)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x_1, x_2, . . . , x_{100} be real numbers.
If x_1 + 2x_2 + . . . + 100x_{100} = 1,
then find the minimum value of x_1/1 + x_2/2 + . . . + x_{100}/100.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First, the problem is posed incorrectly.
Indeed, let's consider the simpler case of 2D problem.
Let x and y be real numbers. If x + 2y = 1,
then find the minimum value of 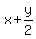 .
In this case, x = 1 - 2y, and the objective function is .
In this case, x = 1 - 2y, and the objective function is
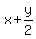 = = 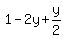 = =  .
But it is clear, that without additional constraints,
this linear objective function DOES NOT HAVE MINIMUM. .
But it is clear, that without additional constraints,
this linear objective function DOES NOT HAVE MINIMUM.
Consider another case, next in its complexity: 3D case.
Let x, y and z be real numbers. If x + 2y + 3z = 1,
then find the minimum value of  .
In this case, again, x = 1 - 2y - 3z, and the objective function is .
In this case, again, x = 1 - 2y - 3z, and the objective function is
 = = 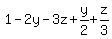 = =  .
But it is clear, that without additional constraints,
this linear objective function DOES NOT HAVE MINIMUM. .
But it is clear, that without additional constraints,
this linear objective function DOES NOT HAVE MINIMUM.
Similarly, in the problem's 100-dimensional case, the given linear objective function also HAS NO MINIMUM.
So, as it is printed in the post, the problem is posed mathematically INCORRECTLY,
has no solution and does not make sense.
In particular, all the tricks by @CPhill in his post are INCORRECT and IRRELEVANT,
since they ALL go out the target. In simple words, the "solution" by @CPhill is CONCEPTUALLY WRONG.
In order for the problem would make sense, its formulation SHOULD BE CHANGED.
The correct formulation is THIS:
Let x_1, x_2, . . . , x_{100} be real  numbers.
If x_1 + 2x_2 + . . . + 100x_{100} = 1,
then find the minimum value of x_1/1 + x_2/2 + . . . + x_{100}/100. numbers.
If x_1 + 2x_2 + . . . + 100x_{100} = 1,
then find the minimum value of x_1/1 + x_2/2 + . . . + x_{100}/100.
In this formulation, the problem is
a standard Linear Programming problem,
and it has nice standard LP-solution.
Below is my solution for this MODIFIED FORMULATION.
In this problem, we have a 99-dimensional hyperplane in 100-dimensional space,
defined by the given equation
 + +  + . . . + + . . . +  = 1
(the constraint) and the objective function to minimize = 1
(the constraint) and the objective function to minimize
 + +  + . . . + + . . . +  .
From this point of view, it is a standard LP-programming minimization problem.
The minimum is achieved in some corner point.
The corner points are .
From this point of view, it is a standard LP-programming minimization problem.
The minimum is achieved in some corner point.
The corner points are
 = (1, 0, 0, . . . , 0), = (1, 0, 0, . . . , 0),
 = (0, 1/2, 0, . . . , 0), = (0, 1/2, 0, . . . , 0),
 = (0. 0, 1/3, . . . , 0),
. . . . . . . . . . . = (0. 0, 1/3, . . . , 0),
. . . . . . . . . . .
 = (0, 0, 0, . . . , 1/100).
The minimum of the given linear function is achieved in some corner point, and, OBVIOUDLY,
this point is = (0, 0, 0, . . . , 1/100).
The minimum of the given linear function is achieved in some corner point, and, OBVIOUDLY,
this point is
 = (0, 0, 0, . . . , 1/100)
With the minimum value of = (0, 0, 0, . . . , 1/100)
With the minimum value of  = =  = = 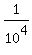 = 0.0001.
ANSWER. Under given conditions, the minimum value of x_1/1 + x_2/2 + . . . + x_{100}/100
is = 0.0001.
ANSWER. Under given conditions, the minimum value of x_1/1 + x_2/2 + . . . + x_{100}/100
is  = = 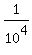 = 0.0001. = 0.0001.
Solved.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|