SOLUTION: Find all real x where 2 \cdot \frac{x - 5}{x - 3} > \frac{2x - 5}{x + 2} + 20. Give your answer in interval notation.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Find all real x where 2 \cdot \frac{x - 5}{x - 3} > \frac{2x - 5}{x + 2} + 20. Give your answer in interval notation.       Log On


   

Question 1209883: Find all real x where
2 \cdot \frac{x - 5}{x - 3} > \frac{2x - 5}{x + 2} + 20.
Give your answer in interval notation.
Answer by greenestamps(13195) About Me  (Show Source):
You can put this solution on YOUR website!


2%28%28x-5%29%2F%28x-3%29%29%3E%282x-5%29%2F%28x%2B2%29%2B20

Modify the inequality to have all non-zero terms on the left:

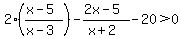
2%28%28x-5%29%2F%28x-3%29%29-%282x-5%29%2F%28x%2B2%29-20%3E0

Combine terms with the common denominator and simplify:





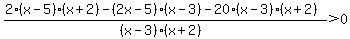
%282x%5E2-6x-20-2x%5E2%2B11x-15-20x%5E2%2B20x%2B120%29%2F%28%28x-3%29%28x%2B2%29%29%3E0

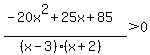
%28-20x%5E2%2B25x%2B85%29%2F%28%28x-3%29%28x%2B2%29%29%3E0

Multiply everything by -1 to make the leading coefficient of the numerator positive -- flipping the direction of the inequality:

%2820x%5E2-25x-85%29%2F%28%28x-3%29%28x%2B2%29%29%3C0

[1] 5%284x%5E2-5x-17%29%2F%28%28x-3%29%28x%2B2%29%29%3C0

The zeros of the numerator are 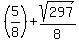%285%2F8%29%2Bsqrt%28297%29%2F8%29 and %285%2F8%29-sqrt%28297%29%2F8%29, or approximately -1.5292 and 2.7792. For convenience, call these roots A and B.

The zeros of the denominator are -2 and 3.

The zeros of the numerator and denominator (the "critical points") divide the values of x into 5 regions:
1. (-infinity,-2)
2. (-2,A]
3. [A,B]
4. [B,3)
5. (3,infinity)

Using the test point x=0 in [1], which is in interval 3, we see that the inequality is NOT satisfied on that interval. Then since the sign of the rational expression changes at each critical point, we find that the given inequality is satisfied on intervals 2 and 4.

ANSWER: (-2,A] U [B,3)