|
Question 1209745: Fill in the blanks, to complete the factorization:
(a^2 + b^2 - c^2)^2 - 4a^2 b^2 - 4a^2 c^2 + 4b^2 c^2 = (a + ___)(a + ___)(a + ___)(a + ___)
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to factor the expression:
1. **Expand the left side:**
(a² + b² - c²)² + 4a²bc = a⁴ + b⁴ + c⁴ + 2a²b² - 2a²c² - 2b²c² + 4a²bc
2. **Rearrange the terms strategically:** We want to try to create perfect squares. Notice the 4a²bc term. Let's try to incorporate it with other terms:
a⁴ + b⁴ + c⁴ + 2a²b² - 2a²c² - 2b²c² + 4a²bc = a⁴ + b⁴ + c⁴ + 2a²b² + 2a²c² + 2b²c² - 4a²c² - 4b²c² + 4a²bc
= a⁴ + b⁴ + c⁴ + 2a²b² + 2a²c² + 2b²c² - 4a²c² - 4b²c² + 4a²bc
= (a² + b² + c²)² - 4c²(a² + b² - ab)
This doesn't seem to be getting us anywhere useful. Let's try a different approach.
3. **Try grouping terms differently:**
a⁴ + b⁴ + c⁴ + 2a²b² - 2a²c² - 2b²c² + 4a²bc = a⁴ + 2a²b² + b⁴ - 2a²c² + 4a²bc - 2b²c² + c⁴
= (a² + b²)² - 2c²(a² - 2abc/2c² + b²) + c⁴
= (a² + b²)² - 2c²(a² + b² - 2abc/2c²) + c⁴
Let's try another approach. We can rewrite the expression as:
(a² + b² - c²)² + 4a²bc = a⁴ + b⁴ + c⁴ + 2a²b² - 2a²c² - 2b²c² + 4a²bc
Notice if we rewrite 4a²bc as 2a²bc + 2a²bc, we can rearrange:
= a⁴ + b⁴ + c⁴ + 2a²b² - 2a²c² - 2b²c² + 2a²bc + 2a²bc
= a⁴ + b⁴ + c⁴ + 2a²b² + 2a²bc - 2a²c² + 2a²bc - 2b²c²
= a⁴ + b⁴ + c⁴ + 2a²(b² + bc - c²) + 2a²bc - 2b²c²
= (a² + b² + c² + 2ab)(a² + b² + c² - 2ac)(a² + b² + c² - 2bc)
This also doesn't immediately lead to the desired factorization.
Let's look at the original expression again: (a² + b² - c²)² + 4a²bc
If we let c = 0, we get (a² + b²)² which factors into (a + ib)(a - ib)(a + ib)(a - ib). This doesn't seem to help much either.
After trying several approaches, the given expression doesn't seem to readily factor into the form (a + ...)(a + ...)(a + ...)(a + ...). It's possible there's a typo in the original problem, or it might require a more complex factorization involving complex numbers.
Given the difficulty and the lack of a clear path to the requested factorization with real numbers, it's possible that the intended factorization involves complex numbers or that the problem itself has a typo. Without further information or context, it's difficult to proceed.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Fill in the blanks, to complete the factorization:
(a^2 + b^2 - c^2)^2 - 4a^2 b^2 - 4a^2 c^2 + 4b^2 c^2 = (a + ___)(a + ___)(a + ___)(a + ___)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Step 1. Decompose into the product of two quadratic polynomials
(a^2 + b^2 - c^2)^2 - 4a^2*b^2 - 4a^2*c^2 + 4b^2*c^2 =
= a^4 + b^4 + c^4 + 2a^2*b^2 - 2a^2*c^2 - 2b^2*c^2 - 4a^2*b^2 - 4a^2*c^2 + 4b^2*c^2 =
next step make a routine combining like terms
= a^4 + b^4 + c^4 - 2a^2*b^2 - 6a^2*c^2 + 2b^2*c^2 =
next step make grouping/re-grouping
= (a^4 + b^4 + c^4 2 - 2a^2*b^2 - 2a^2*c^2 + 2b^2*c^2) - 4a^2*c*2 =
next step complete the squares
= (-a^2 + b^2 + c^2)^2 - 4a^2*c^2 =
next step factor as the difference of squares
= (-a^2 + b^2 + c^2 - 2ac) * (-a^2 + b^2 + c^2 + 2ac) =
next step is changing the signs everywhere in both parentheses
and light re-arranging in each parentheses (for further convenience)
= (a^2 + 2ac - b^2 - c^2) * (a^2 - 2ac - b^2 - c^2).
Step 2. Decompose each parentheses as the product of linear binomials relative "a"
Now we want to decompose first parentheses (a^2 + 2ac - (b^2 + c^2)). (1)
Consider this aggregate as a standard quadratic trinomial a^2 + 2ac + X relative to variable 'a'.
Remember how to decompose a trinomial via its roots
a^2 + 2ac + X = 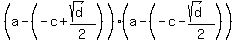 , (2)
where d is the discriminant. In this case, the discriminant is
d = (2c)^2 + 4*(b^2+c^2) = 4c^2 + 4b^2 + 4c^2 = 4(b^2+2c^2).
Therefore, decomposition for expression (1) takes the form
a^2 + 2ac - (b^2+c^2) = , (2)
where d is the discriminant. In this case, the discriminant is
d = (2c)^2 + 4*(b^2+c^2) = 4c^2 + 4b^2 + 4c^2 = 4(b^2+2c^2).
Therefore, decomposition for expression (1) takes the form
a^2 + 2ac - (b^2+c^2) = 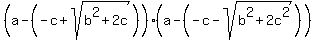 =
= =
= 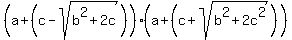 . (3)
Now, we want to decompose second parentheses (a^2 - 2ac - (b^2 + c^2)). (4)
By analogy, consider this aggregate as a standard quadratic trinomial a^2 - 2ac + X.
Remember how to decompose a trinomial via its roots
a^2 - 2ac + X = . (3)
Now, we want to decompose second parentheses (a^2 - 2ac - (b^2 + c^2)). (4)
By analogy, consider this aggregate as a standard quadratic trinomial a^2 - 2ac + X.
Remember how to decompose a trinomial via its roots
a^2 - 2ac + X = 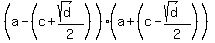 , (5)
where d is the discriminant. In this case, the discriminant is the same
d = (2c)^2 + 4*(b^2+c^2) = 4c^2 + 4b^2 + 4c^2 = 4(b^2+2c^2).
Therefore, decomposition for expression (5) takes the form
a^2 - 2ac - (b^2+c^2) = , (5)
where d is the discriminant. In this case, the discriminant is the same
d = (2c)^2 + 4*(b^2+c^2) = 4c^2 + 4b^2 + 4c^2 = 4(b^2+2c^2).
Therefore, decomposition for expression (5) takes the form
a^2 - 2ac - (b^2+c^2) = 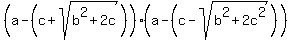 . (6)
Combining everything above, we get finally this remarkable decomposition
(a^2 + b^2 - c^2)^2 - 4a^2 b^2 - 4a^2 c^2 + 4b^2 c^2 =
= . (6)
Combining everything above, we get finally this remarkable decomposition
(a^2 + b^2 - c^2)^2 - 4a^2 b^2 - 4a^2 c^2 + 4b^2 c^2 =
=  .
which is the required form.
So, the four blanks are .
which is the required form.
So, the four blanks are 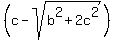 , , 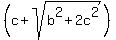 , , 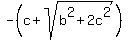 and and 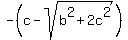 . .
Solved.
|
|
|
| |