Question 1209722: Let p, q, r, and s be the roots of g(x) = 3x^4 - 8x^3 + 5x^2 + 2x - 17 - 2x^4 + 10x^3 + 11x^2 + 18x - 14.
Compute \frac{1}{p} + \frac{1}{q} + \frac{1}{r} + \frac{1}{s}.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
Hint #1
Combine like terms. Simplify the polynomial as much as possible before moving on.
Hint #2
Hint #3
Use Vieta's Formulas.
See this similar question
The specific formulas you'll need are:
where a through e are coefficients from ax^4+bx^3+cx^2+dx+e
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
Let p, q, r, and s be the roots of g(x) = 3x^4 - 8x^3 + 5x^2 + 2x - 17 - 2x^4 + 10x^3 + 11x^2 + 18x - 14.
Compute 1/p + 1/q + 1/r + 1/s.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There is another method to solve, so beautiful that
the blind begin to walk and the mute begin to see.
Notice that since the constant term is not zero,
no one root p, q, r or s is zero.
Reduce the given equation to the standard form combining like terms. You will get
g(x) = x^4 + 2x^3 + 16x^2 + 20x - 31. (1)
Divide this reduced equation by x^4. You will get another polynomial (like a sock turned inside out)
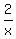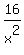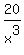 +  +  +  -  . (2)
If some value p, q, r, s is the root to polynomial (1),
then 1/p, 1/q, 1/r, 1/s is the zero of function (2).
Let's consider now the polynomial
h(y) = 1 + 2y + 16y^2 + 20y^3 - 31y^4. (3)
Compare (3) with (2) and recognize that (3) is the same expression as (2) with replaced '1/x' by 'y'.
Since p, q, r and s are the roots for polynomial (1),
1/p, 1/q, 1/r and 1/s are the roots for polynomial (3).
Now apply Vieta's theorem and find that the sum of the roots 1/p, 1/q, 1/r, 1/s
is equal to the coefficient 20 at y^3 in polynomial (3), divided by the leading coefficient -31 at y^4,
taken with the opposite sign
1/p + 1/q + 1/r + 1/s =  =  .
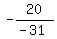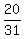At this point, the problem is solved in full, without making cumbersome calculations.
ANSWER. 1/p + 1/q + 1/r + 1/s = .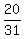
Isn't it beautiful ?
This method is called "turning a polynomial inside out".
Turning a polynomial inside out can be done mentally,
so one can write an answer immediately, without making/writing these reasons on paper.
If you show this focus-pocus to your teacher/professor or at the interview,
the other side will be shocked to see such an elegant solution.
|
|
|
