Question 1205720: what is the remainder when P(x)=x^(2)+5 is divided by (x+1)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x^2 + 5 is equal to (x + 1) * (x - 1) with a remainder of 6.
(x + 1) * (x - 1) = x^2 - 1
add the remainder of 6 to that and you get x^2 + 5.
the divisor is x + 1
the dividend is x^2 + 5
the quotient is x - 1 with a remainder of 6.
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
what is the remainder when P(x)=x^(2)+5 is divided by (x+1)
~~~~~~~~~~~~~~~~~~~~~~
I will show you two ways of solving this problem.
First way: using the remainder theorem
According to the Remainder theorem, the remainder of division any polynomial P(x)
by a binomial (x-a), where "a" is a real (or integer) number, is the value
of the polynomial P(x) at x= a, i.e. P(a).
In this problem, a= -1, so, according to the Remainder theorem, the remainder
of division P(x) = x^2+5 by (x+1) is P(-1) = (-1)^2 + 5 = 6.
ANSWER. The remainder of division P(x) = x^2+5 by (x+1) is 6.
Second way: using explicit division via grouping
Using grouping, we can write
P(x) =  = = 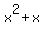 + + 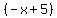 = x(x+1) + (-x-1) + 1 + 5 = x(x+1) - (x+1) + 6 =
= (x+1)*(x-1) + 6.
It shows that when P(x) is divided by (x+1), the quotient is (x-1) and the remainder is 6.
Thus the ANSWER is the same as in the first solution above. = x(x+1) + (-x-1) + 1 + 5 = x(x+1) - (x+1) + 6 =
= (x+1)*(x-1) + 6.
It shows that when P(x) is divided by (x+1), the quotient is (x-1) and the remainder is 6.
Thus the ANSWER is the same as in the first solution above.
Solved in two ways for your better understanding.
--------------
Surely, there is third way, which is direct long division of polynomials.
This method is straightforward and purely mechanical procedure - therefore,
I do not say more about it and even do not show it here.
|
|
|