SOLUTION: Using the foil method, I cant seem to figure this one out. Please help... 2x^2+5x-6

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Using the foil method, I cant seem to figure this one out. Please help... 2x^2+5x-6      Log On


   

Question 117937: Using the foil method, I cant seem to figure this one out. Please help...
2x^2+5x-6
Found 2 solutions by jim_thompson5910, bucky:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Do you want to factor this?



Looking at 2x%5E2%2B5x-3 we can see that the first term is 2x%5E2 and the last term is -3 where the coefficients are 2 and -3 respectively.

Now multiply the first coefficient 2 and the last coefficient -3 to get -6. Now what two numbers multiply to -6 and add to the middle coefficient 5? Let's list all of the factors of -6:



Factors of -6:
1,2,3,6

-1,-2,-3,-6 ...List the negative factors as well. This will allow us to find all possible combinations

These factors pair up and multiply to -6
(1)*(-6)
(2)*(-3)
(-1)*(6)
(-2)*(3)

note: remember, the product of a negative and a positive number is a negative number


Now which of these pairs add to 5? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 5

First NumberSecond NumberSum
1-61+(-6)=-5
2-32+(-3)=-1
-16-1+6=5
-23-2+3=1



From this list we can see that -1 and 6 add up to 5 and multiply to -6


Now looking at the expression 2x%5E2%2B5x-3, replace 5x with -1x%2B6x (notice -1x%2B6x adds up to 5x. So it is equivalent to 5x)

2x%5E2%2Bhighlight%28-1x%2B6x%29%2B-3


Now let's factor 2x%5E2-1x%2B6x-3 by grouping:


%282x%5E2-1x%29%2B%286x-3%29 Group like terms


x%282x-1%29%2B3%282x-1%29 Factor out the GCF of x out of the first group. Factor out the GCF of 3 out of the second group


%28x%2B3%29%282x-1%29 Since we have a common term of 2x-1, we can combine like terms

So 2x%5E2-1x%2B6x-3 factors to %28x%2B3%29%282x-1%29


So this also means that 2x%5E2%2B5x-3 factors to %28x%2B3%29%282x-1%29 (since 2x%5E2%2B5x-3 is equivalent to 2x%5E2-1x%2B6x-3)

-------------------------------
Answer:

So 2x%5E2%2B5x-3 factors to %28x%2B3%29%282x-1%29

Answer by bucky(2189) About Me  (Show Source):
You can put this solution on YOUR website!
First notice that the coefficients and the constant term are 2, 5, and 6. They do not have common
factors (other than 1, of course) so you can not pull out a common numeric factor. Therefore,
you begin by examining the first term of the expression and you notice that 2x^2 can only
factor to 2x*x. So set up two sets of parentheses:
.
(2x _____)*(x _____)
.
What goes into the blanks in these parentheses must be a pair of factors of 6, the constant term
in the polynomial. There are only two factor pairs of 6 as follows:
.
1 and 6 or
2 and 3
.
Since the 6 in the polynomial has a negative sign, one of the numbers in each pair of factors
must have a negative sign.
.
Anyhow, this means that there are 4 possible factors of the original polynomial as follows:
.
(2x 1)*(x 6) or
(2x 6)*(x 1) or
(2x 2)*(x 3) or
(2x 3)*(x 2)
.
In addition in each of these 4 possibilities we need to decide where the plus and minus signs go.
.
In the first possible solution the 6 multiplies the 2x to give 12x and the 1 multiplies
the x to give just x. There is no way that 12x and x can be combined to give the 5x in the
original polynomial. Therefore, this first possible solution (2x 1)*(x 6) will not work because
it cannot be multiplied out to give the original polynomial.
.
The second possible solution (2x 6)*(x 1) will also not work. The 6 multiplies the x to give 6x
and the 1 multiplies the 2x to give 2x. There is no way that 6x and 2x can be combined to
give 5x. Therefore, disregard this possibility.
.
In the third possible solution (2x 2)*(x 3) the 3 multiplies the 2x to give 6x and the 2 multiplies
the x to give 2x. There is no way 6x and 2x can be added or subtracted to give 5x.
.
The fourth and final possibility is (2x 3)*(x 2). In this pair of factors the 2 multiplies 2x
to give 4x. And the 3 multiplies the x to give 3x. There is no way that 2x and 4x can be
combined by addition or subtraction to give the +5x of the original polynomial.
.
What does this all mean???? It means that the polynomial 2x^2 + 5x - 6 does not factor nicely.
.
The quadratic formula can be used to factor 2x^2 + 5x - 6 into two "binomial" factors.
.
2x^2 + 5x - 6 = 0 is in the standard form ax^2 + bx + c = 0. By comparing these two you can
see that for your problem a = 2, b = 5, and c = -6. According to the quadratic formula, the
answer for x is:
.
x+=+-b%2F%282%2Aa%29+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%2F%282%2Aa%29+
.
For your answers substitute the values of a, b, and c to get:
.
x+=+-%28%2B5%29%2F%282%2Aa%29+%2B-+sqrt%28+5%5E2-4%2A2%2A%28-6%29%29%2F%282%2A2%29+
.
The constants inside the radical compute to be:
.
25 + 48 = 73
.
This makes the radical become the square root of 73. the -(+5) is just -5 and in the denominator
the 2*2 is 4. Substituting all these results gives:
.
x+=+-5%2F4+%2B-+sqrt%28+73%29%2F4+
.
Subtracting 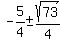-5%2F4+%2B-+sqrt%28+73%29%2F4+ from both sides results (one at a time) gives:
.
x+%2B+5%2F4+%2B+sqrt%28+73%29%2F4+=+0 and
.
x+%2B+5%2F4+-+sqrt%28+73%29%2F4+=+0
.
This means that factors of the left side of 2x%5E2+%2B+5x+-+6+=+0 are:
.
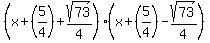
%28x+%2B+%285%2F4%29+%2B+sqrt%28+73%29%2F4%29%2A%28x+%2B+%285%2F4%29+-+sqrt%28+73%29%2F4%29
.
If you multiply these two factors together you get:
.
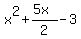
x%5E2+%2B+%285x%29%2F2+-+3
.
This is half of what you need to get back to the original equation. So you can add a factor of 2
to get that the factored form is:
.

.
A solution to the problem, but not the easy version of having two binomials as factors.
.
A little complex, but maybe this is something that will work for you.
.