Question 1179209: Resolve 3x²+1/(x-2)²(x²+2x+2) to partial fraction
Found 3 solutions by MathLover1, Edwin McCravy, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The first tutor misunderstood what was to be done.
The second tutor rewrote the equation wrong so worked a different problem.
--------------------------------------------------------------------------------------
The fraction to be decomposed is
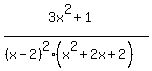
From the basic rules for decomposing fractions, the decomposition will be of the form

The standard procedure for doing the decomposition is to multiply the equation by the LCD:

Note that the second tutor in his work substituted "convenient" values for x to get equations in A, B, C, and D. That turns out to give a quick path to the solution in many problems like this; but it doesn't appear to me to be advantageous in this example.
So another standard method for getting equations in A, B, C, and D is to expand the expression on the right and equate coefficients on the two sides of the equation.


Equating the coefficients of the different degree terms on the two sides of the equation gives us four equations in A, B, C, and D:
(1) A+C=0
(2) B-4C+D=3
(3) -2A+2B+4C-4D=0
(4) -4A+2B+4D=1
Solve (1) to get C=-A and substitute in (2), (3), and (4):
(5) 4A+B+D=3
(6) -6A+2B-4D=0
(7) -4A+2B+4D=1
Eliminate D between (5) and (6), and between (6) and (7):
(8) 10A+6B=12
(9) -10A+4B=1
Add those two equations to eliminate A and solve for B:
(10) 10B=13; B=13/10
Substitute (10) in (8) and solve for A:
10A+78/10=12
100A+78=120
100A=42
(11) A = 42/100 = 21/50
Use (1) and (11) to get C = -21/50
Use (5), (10), and (11) to find D:
84/50+65/50+D=3
D=1/50
We have values for all the unknowns:
A=21/50
B=13/10
C=-21/50
D=1/50
ANSWER:

|
|
|