Question 116758This question is from textbook Intermediate Algebra
: Please help me solve this equation. 
This question is from textbook Intermediate Algebra
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! This is not an equation. This is a polynomial expression. As it stands, there is no solution -- you can't 'solve' a polynomial expression.
So, let's presume that you actually meant to say 'Please solve:  .
The first thing you can do is factor  out of the left side leaving you with:
That gives us two of the five roots directly, namely  and
From here on it gets mighty ugly. Looking at a graph of the cubic factor, we can see that we have one real root, slightly smaller than 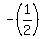 and a conjugate pair of complex roots.
My recommendation, to the extent that your instructor will be satisfied with a reasonable approximation, is to go to a website that has a general cubic equation solver. When you use such a thing, just be sure to remember that the c coefficient in  has a zero value in this problem.
There is another possibility that occurred to me -- you may have a typo in your polynomial. If you actually meant  , then  becomes:
 and we are left with a much easier to handle quadratic.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case  ) has the following solutons:
For these solutions to exist, the discriminant  should not be a negative number.
First, we need to compute the discriminant :  .
The discriminant -467 is less than zero. That means that there are no solutions among real numbers.
If you are a student of advanced school algebra and are aware about imaginary numbers, read on.
In the field of imaginary numbers, the square root of -467 is + or -  .
The solution is 
Here's your graph:
 |
Not nearly as messy, even though the roots are complex.
Hope this helps.
|
|
|
