SOLUTION: Describe the transformations on the following graph of f(x)=e^x. State the placement of the horizontal asymptote and y-intercept after the transformation. For example, “left

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Describe the transformations on the following graph of f(x)=e^x. State the placement of the horizontal asymptote and y-intercept after the transformation. For example, “left       Log On


   

Question 116018: Describe the transformations on the following graph of f(x)=e^x.
State the placement of the horizontal asymptote and y-intercept after the transformation. For example, “left 1” or “rotated about the y-axis” are descriptions.

b) h(x)=e^(-x)
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
b)

Description of transformation:

Looking at h%28x%29=e%5E%28-x%29, notice how the exponent is negated. So let's see what affect this transformation has on f%28x%29=e%5Ex,

h%28x%29=e%5E%28-x%29 Start with the given transformation


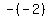h%28-2%29=e%5E%28-%28-2%29%29 Plug in x=-2


h%28-2%29=e%5E%282%29 Negate -%28-2%29 to get 2


Notice if we plug in x=2 into f%28x%29=e%5Ex, we get f%282%29=e%5E2

--------

h%28x%29=e%5E%28-x%29 Start with the given transformation


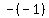h%28-1%29=e%5E%28-%28-1%29%29 Plug in x=-1


h%28-1%29=e%5E%281%29 Negate -%28-1%29 to get 1

h%28-1%29=e Remove the exponent of 1

Notice if we plug in x=1 into f%28x%29=e%5Ex, we get f%281%29=e%5E1=e


So if we take the opposite of x (to get -x), and plug that into g(x), we'll get the same f(x) answer.


----------------------------------
Answer:
So what this does is simply reflect the entire graph over the y-axis

Notice if we graph f%28x%29 and g%28x%29, we get

+graph%28+500%2C+500%2C+-10%2C+10%2C+-10%2C+10%2C+exp%28x%29%2Cexp%28-x%29%29+ Graph of f%28x%29=e%5Ex (red) and h%28x%29=e%5E%28-x%29 (green)

and we can visually verify the transformation



Horizontal Asymptote:

Since we reflected the graph with respect to the y-axis, the horizontal asymptote of h%28x%29=e%5E%28-x%29 is the same as f%28x%29=e%5Ex (you can see this from the graph above)
----------------------------------
Answer:
So the horizontal asymptote is y=0

Note: you can visually verify this answer by looking at the graph above

y-intercept in (x, y) form:

Since the line of symmetry between the two graphs is the line x=0 (ie the y axis), this means that the point that intersects with the y-axis is reflected to itself. So essentially the y-intercept does not change also. Once again, you can visually verify this using the graph above.

----------------------------------
Answer:
So the y-intercept is (0,1)

Once again, you can visually verify this answer by looking at the graph above