Question 115752: Factor these ?
4x^2 -12x -40
2x^2 -16x +30
Found 2 solutions by Gator Tutoring, jim_thompson5910:
Answer by Gator Tutoring(5)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.Factor, 2x^2 -16x +30
set up parenthesis
( + ) * ( + )
what 2 numbers multiply to give you 2x^2?
place those numbers here:
( NUM + ) * ( NUM + )
( 2x + ) * ( x + )
what 2 numbers multiply to give you 30?
place those numbers here:
( + NUM ) * ( + NUM )
( 2x - 10 ) * ( x - 3 )
note that I changed the signs from positive to negative.
Answer:
( 2x - 10 ) * ( x - 3 )
to check if answer is correct:
If you multiply this out you will get
2x^2 -16x +30
note:
Understand that this method requires you to pick
a couple of numbers and see if they work. If they do not work then pick another two. also note that the signs (+/-) also may need to be changed.
Gator Tutoring
pichonz@gmail.com
Getting Math help couldn't get any easier.
How?
1. Email me all your questions (minimum of 5)
2. I post worked out solutions on Google/Amazon/Ebay
3. You purchase, I send file through email.
Costs:
Standard = Worked out solutions
Premium = Worked out solutions + strategies + definitions + comments. Answers from above are done using the premium service.
Standard > $1 per problem
Premium > $2 per problem
note: Problems with multiple questions are counted as separate problems.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! #1
Looking at 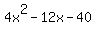 we can see that the first term is we can see that the first term is  and the last term is and the last term is  where the coefficients are 4 and -40 respectively. where the coefficients are 4 and -40 respectively.
Now multiply the first coefficient 4 and the last coefficient -40 to get -160. Now what two numbers multiply to -160 and add to the middle coefficient -12? Let's list all of the factors of -160:
Factors of -160:
1,2,4,5,8,10,16,20,32,40,80,160
-1,-2,-4,-5,-8,-10,-16,-20,-32,-40,-80,-160 ...List the negative factors as well. This will allow us to find all possible combinations
These factors pair up and multiply to -160
(1)*(-160)
(2)*(-80)
(4)*(-40)
(5)*(-32)
(8)*(-20)
(10)*(-16)
(-1)*(160)
(-2)*(80)
(-4)*(40)
(-5)*(32)
(-8)*(20)
(-10)*(16)
note: remember, the product of a negative and a positive number is a negative number
Now which of these pairs add to -12? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to -12
| First Number | Second Number | Sum | | 1 | -160 | 1+(-160)=-159 | | 2 | -80 | 2+(-80)=-78 | | 4 | -40 | 4+(-40)=-36 | | 5 | -32 | 5+(-32)=-27 | | 8 | -20 | 8+(-20)=-12 | | 10 | -16 | 10+(-16)=-6 | | -1 | 160 | -1+160=159 | | -2 | 80 | -2+80=78 | | -4 | 40 | -4+40=36 | | -5 | 32 | -5+32=27 | | -8 | 20 | -8+20=12 | | -10 | 16 | -10+16=6 |
From this list we can see that 8 and -20 add up to -12 and multiply to -160
Now looking at the expression 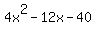 , replace , replace 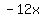 with with 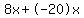 (notice (notice 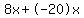 adds up to adds up to 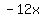 . So it is equivalent to . So it is equivalent to 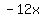 ) )

Now let's factor 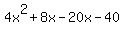 by grouping: by grouping:
 Group like terms Group like terms
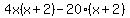 Factor out the GCF of Factor out the GCF of  out of the first group. Factor out the GCF of out of the first group. Factor out the GCF of  out of the second group out of the second group
 Since we have a common term of Since we have a common term of  , we can combine like terms , we can combine like terms
So 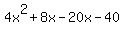 factors to factors to 
So this also means that 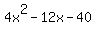 factors to factors to  (since (since 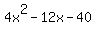 is equivalent to is equivalent to 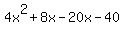 ) )
-------------------------------
Answer:
So 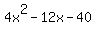 factors to factors to 
#2
Looking at 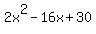 we can see that the first term is we can see that the first term is  and the last term is and the last term is  where the coefficients are 2 and 30 respectively. where the coefficients are 2 and 30 respectively.
Now multiply the first coefficient 2 and the last coefficient 30 to get 60. Now what two numbers multiply to 60 and add to the middle coefficient -16? Let's list all of the factors of 60:
Factors of 60:
1,2,3,4,5,6,10,12,15,20,30,60
-1,-2,-3,-4,-5,-6,-10,-12,-15,-20,-30,-60 ...List the negative factors as well. This will allow us to find all possible combinations
These factors pair up and multiply to 60
1*60
2*30
3*20
4*15
5*12
6*10
(-1)*(-60)
(-2)*(-30)
(-3)*(-20)
(-4)*(-15)
(-5)*(-12)
(-6)*(-10)
note: remember two negative numbers multiplied together make a positive number
Now which of these pairs add to -16? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to -16
| First Number | Second Number | Sum | | 1 | 60 | 1+60=61 | | 2 | 30 | 2+30=32 | | 3 | 20 | 3+20=23 | | 4 | 15 | 4+15=19 | | 5 | 12 | 5+12=17 | | 6 | 10 | 6+10=16 | | -1 | -60 | -1+(-60)=-61 | | -2 | -30 | -2+(-30)=-32 | | -3 | -20 | -3+(-20)=-23 | | -4 | -15 | -4+(-15)=-19 | | -5 | -12 | -5+(-12)=-17 | | -6 | -10 | -6+(-10)=-16 |
From this list we can see that -6 and -10 add up to -16 and multiply to 60
Now looking at the expression 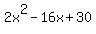 , replace , replace 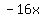 with with 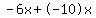 (notice (notice 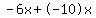 adds up to adds up to 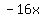 . So it is equivalent to . So it is equivalent to 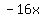 ) )
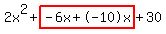
Now let's factor  by grouping: by grouping:
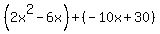 Group like terms Group like terms
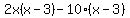 Factor out the GCF of Factor out the GCF of  out of the first group. Factor out the GCF of out of the first group. Factor out the GCF of  out of the second group out of the second group
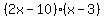 Since we have a common term of Since we have a common term of  , we can combine like terms , we can combine like terms
So  factors to factors to 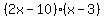
So this also means that 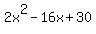 factors to factors to 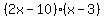 (since (since 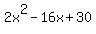 is equivalent to is equivalent to  ) )
-------------------------------
Answer:
So 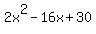 factors to factors to 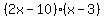
|
|
|