Question 1150638: In certain right triangles √h^2-a^2 = 24, where h represents the length of the hypotenuse and a is the length of one of the legs. Find all possible ordered pairs (h,a), where h, a ∈ N. Explain your reasoning thoroughly. By Spirit of Math.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
Answer by ikleyn(52908)  (Show Source):
You can put this solution on YOUR website! .
From  = 24 we have
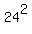 =  = 576
(h-a)*(h+a) = 576.
The divisors of the number 576 are the numbers
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576.
Therefore, we have the series of cases.
1) h - a = 1
h + a = 576
------------------ > no solution in integer positive numbers.
2) h - a = 2
h + a = 288
------------------ > h =  = 145; a = 145-2 = 143.
3) h - a = 3
h + a = 192
------------------ > no solution in integer positive numbers.
4) h - a = 4
h + a = 144
------------------ > h =  = 74; a = 74-4 = 70.
Moving in this way further along the row of divisors of the number 576 till the number h = 18 inclusive,
you will consider all the cases and will get all other possible (and/or impossible) solutions.
Since I don't want to deprive you this joy, I will leave you at this point.
|
|
|
