Question 1124747: The roots of the polynomial equation 2x^3 - 8x^2 + 3x + 5 = 0 are alpha, beta and gamma.
Find the polynomial equation with roots alpha^2, beta^2, gamma^2
Any help is so much appreciated!
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The roots of the polynomial equation 2x^3 - 8x^2 + 3x + 5 = 0 are alpha, beta and gamma.
Find the polynomial equation with roots alpha^2, beta^2, gamma^2
~~~~~~~~~~~~~~~
The given equation
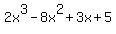 = 0 (1)
is equivalent to = 0 (1)
is equivalent to
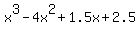 = 0 (2) (all the coefficients of (1) are divided by 2)
Equation (2) has the same roots = 0 (2) (all the coefficients of (1) are divided by 2)
Equation (2) has the same roots  , ,  and and  as equation (1). Therefore, as equation (1). Therefore,
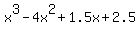 = = 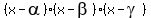 , (3)
and, according to Vieta's theorem , (3)
and, according to Vieta's theorem
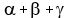 = 4, = 4,  = 1.5, = 1.5, 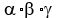 = -2.5. (4)
Now, an equation with the roots = -2.5. (4)
Now, an equation with the roots 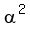 , , 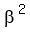 and and  is is
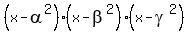 = 0. (5)
By the Vieta's theorem (or by applying FOIL directly), the coefficients of the left side polynomial are = 0. (5)
By the Vieta's theorem (or by applying FOIL directly), the coefficients of the left side polynomial are
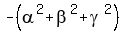 at x^2; (6) at x^2; (6)
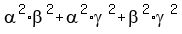 at x; and (7) at x; and (7)
 as the constant term. (8)
So, my task now is to express the coefficient (6), (7) and (8) via the coefficients (4) of the equation (2).
Regarding as the constant term. (8)
So, my task now is to express the coefficient (6), (7) and (8) via the coefficients (4) of the equation (2).
Regarding  , it is easy: , it is easy:
 = =  = = 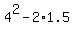 = 16-3 = 13.
So, the coefficient at x^2 of the polynomial (5) is = 16-3 = 13.
So, the coefficient at x^2 of the polynomial (5) is 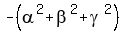 = -13.
Regarding = -13.
Regarding  , it is easy, too : , it is easy, too :
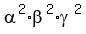 = = 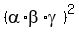 = = 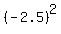 = 6.25.
So, the constant term of the polynomial (5) is = 6.25.
So, the constant term of the polynomial (5) is 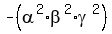 = -6.25.
Regarding = -6.25.
Regarding 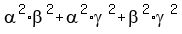 , it is slightly more long way : , it is slightly more long way :
 = 1.5 of (4) implies (squaring both sides)
2.25 = = 1.5 of (4) implies (squaring both sides)
2.25 =  =
= =
= 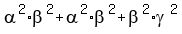 + + 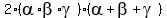 = substituting the known values from (4) =
= = substituting the known values from (4) =
= 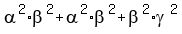 + 2*(-2.5)*4,
which implies + 2*(-2.5)*4,
which implies
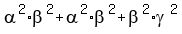 = 2.25 + 20 = 22.25.
Thus we know all three coefficients of the polynomial (5) = 2.25 + 20 = 22.25.
Thus we know all three coefficients of the polynomial (5)
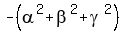 = -13 at x^2; = -13 at x^2;
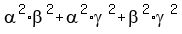 = 22.25 at x; and = 22.25 at x; and
 = -6.25 as the constant term.
Answer. The polynomial equation under the question is = -6.25 as the constant term.
Answer. The polynomial equation under the question is 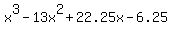 = 0. = 0.
********************
* * * SOLVED. * * *
********************
|
|
|