Question 1116168: Solve 2/x≤x/2
Is the solution (-00,-2)U(0,2)?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39631)   (Show Source): (Show Source):
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
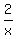 <= <=  (1) (1)
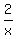 - -  <= <= 
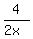 - - 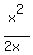 <= <=  (written with the common denominator 2x ) (written with the common denominator 2x )
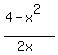 <= <= 
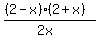 <= <=  (2)
On the left side, we have a rational function of the three factors (2-x), (2+x) and (2x).
There are three critical values, where the factor become equal to zero and change their sign: -2, 0, and 2.
And there are four interval to analyse: a) x < -2; b) -2 <= x < 0; c) 0 < x < 2; and d) x >= 2.
In the interval a) x < - 2 factors (x+2) and (2x) are negative; factor (2-x) is positive. So inequality (2) is FALSE.
In the interval b) -2 <= x < 0 the factor (x+2) is positive, factor (2x) is negative; factor (2-x) is positive.
So, the whole function in the left side of (2) is negative, and the inequality (2) IS TRUE.
In the interval c) 0 < x < 2 the factors (x+2) and (2x) are positive; the factor (x-2) is positive; so inequality (2) is FALSE.
In the interval d) x >= 2 factors (x+2) and (2x) are positive; factor (2-x) is negative. So, the whole function in the left side of (2) is negative, and the inequality (2) IS TRUE.
Thus the inequality (2) is TRUE in these two intervals
-2 <= x < 0 and x >= 2.
Since inequalities (1) and (2) are EQUIVALENT (!), your answer is:
Answer. The original inequality is true at -2 <= x < 0 and x >= 2.
The solution is the set [ (2)
On the left side, we have a rational function of the three factors (2-x), (2+x) and (2x).
There are three critical values, where the factor become equal to zero and change their sign: -2, 0, and 2.
And there are four interval to analyse: a) x < -2; b) -2 <= x < 0; c) 0 < x < 2; and d) x >= 2.
In the interval a) x < - 2 factors (x+2) and (2x) are negative; factor (2-x) is positive. So inequality (2) is FALSE.
In the interval b) -2 <= x < 0 the factor (x+2) is positive, factor (2x) is negative; factor (2-x) is positive.
So, the whole function in the left side of (2) is negative, and the inequality (2) IS TRUE.
In the interval c) 0 < x < 2 the factors (x+2) and (2x) are positive; the factor (x-2) is positive; so inequality (2) is FALSE.
In the interval d) x >= 2 factors (x+2) and (2x) are positive; factor (2-x) is negative. So, the whole function in the left side of (2) is negative, and the inequality (2) IS TRUE.
Thus the inequality (2) is TRUE in these two intervals
-2 <= x < 0 and x >= 2.
Since inequalities (1) and (2) are EQUIVALENT (!), your answer is:
Answer. The original inequality is true at -2 <= x < 0 and x >= 2.
The solution is the set [ , , ) U [ ) U [ , , ]. ].
Solved.
------------
To see many other similar solved problems for inequalities for rational functions, look into the lesson
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Inequalities".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|