Question 1116164: Graph r(x)=(x-3)^2/x^2-4
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I will guess that you mean 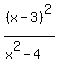 instead of instead of 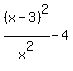 , because the first is far more interesting than the second. , because the first is far more interesting than the second.

The function has a double root at x=3, where the numerator is zero, and vertical asymptotes at x=-2 and x=2, where the denominator is zero.
To get an idea of where the function is positive or negative, imagine "walking" along the x axis left to right, starting at a large negative value of x.
The function consists of 4 linear factors; for large negative values of x, all 4 factors are negative, so the function is positive.
When you pass the vertical asymptote at x = -2, the sign of one of the 4 factors changes, so the function value changes from positive to negative.
At x=2 you pass another vertical asymptote; one factor changes sign; so the function value changes sign again, from negative to positive.
When you pass the zero at x=3, TWO of the 4 factors change sign at the same time, so the function does NOT change sign. The graph touches the x axis but stays positive.
Finally, for the end behavior, observe that for large negative or large positive values of x the function is very close to  ; so the graph has a horizontal asymptote at y=1. ; so the graph has a horizontal asymptote at y=1.
Here is a graph....

|
|
|