Question 1113852: Graph the polynomial p(x)=-2x(x-3)(x+2)^3(x-2)^2
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Graph the polynomial 
For clarification, I will write the polynomial as 
In this form, we can see that the polynomial is of degree 7 with a negative leading coefficient; that means the end behavior of the function is up for large negative x and down for large positive x.
And we can see that, from left to right, the function has
(1) a triple root at x=-2;
(2) a single root at x=0;
(3) a double root at x=2; and
(4) a single root at x=3.
At a single root, the function value changes sign; the graph simply crosses the x axis from positive to negative or vice versa.
At a double root, the sign of the function value does not change; the graph just touches the x axis, like the vertex of a parabola.
At a triple root, the function value changes sign, and the behavior is like the graph of x^3 -- it flattens out but then continues in the same direction.
So with this function, moving left to right, the graph of the function starts positive; at the triple root x=-2, it flattens out but then becomes negative; at the single root x=0, it crosses the x-axis and becomes positive; at the double root x=2 it just touches the x-axis and remains positive; and at the single root x=3 it crosses the x-axis and becomes negative.
Here is a graph:

--------------------------------------------
added at the request of the student: graph

which can be written as
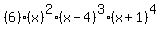
Analysis: degree 9 with positive leading coefficient, so negative for large negative x and positive for large positive x. So, "walking" left to right on the number line....
(1) negative for large negative;
(2) quadruple root at x=-1 (an even power), so the graph just touches the x-axis but the sign of the function does not change -- i.e., it stays negative;
(3) double root at x=0, so again the graph just touches the x-axis at x=0 but the function value remains negative;
(4) triple root at x=4 (an odd degree), so the sign of the function changes to positive; and
(5) there are no more zeros, so the function value remains positive the rest of the way.
A graph:

|
|
|