Question 1105536: Given that 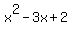 is a factor of is a factor of 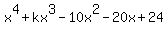 , evaluate the sum of the four roots of the equation: , evaluate the sum of the four roots of the equation: 
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! x^2-3x+2 factors into (x-2)(x-1), so x=1 and 2 are roots.
x^4+kx^3-10x^2-20x+24=0
16+8k-40-40+24=0
8k-40=0
k=5
the polynomial is x^4+5x^3-10x^2-20x+24
synthetic division with 2
2/1===5===-10===-20===24
==1==7=====4=====-12===0
x^3+7x^2+4x-12
-2/1===7===4===-12
==1===5===-6===0
x^2+5x-6, so -2 is a root
(x+6)(x-1)=0, and 1 is already known to be a root, so -6 is the other root.
The sum of -6, -2, 1, 2 is -5. ANSWER.

Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
 = (x-1)*(x-2),
so 1 and 2 are the roots of the given polynomial of the degree 4.
The fact that x= 1 is the root of the given polynomial of the degree 4 means
1^4 +k*1^3 -10*1^2 - 20*1 + 24 = 0, or
1 + k - 10 - 20 + 24 = 0, which implies k = 5.
According to Vieta's theorem, the sum of the roots of the given polynomial of the degree 4 is equal
to the coefficient at x^3 taken with the opposite sign, i.e. -5. = (x-1)*(x-2),
so 1 and 2 are the roots of the given polynomial of the degree 4.
The fact that x= 1 is the root of the given polynomial of the degree 4 means
1^4 +k*1^3 -10*1^2 - 20*1 + 24 = 0, or
1 + k - 10 - 20 + 24 = 0, which implies k = 5.
According to Vieta's theorem, the sum of the roots of the given polynomial of the degree 4 is equal
to the coefficient at x^3 taken with the opposite sign, i.e. -5.
Solved.
|
|
|