|
Question 1104061: Find sin θ if cot θ = - 2 and cos θ < 0.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! cot(T) = 1/tan(T), therefore:
1/tan(T) = -2
solve for tan(T) to get tan(T) = 1/-2 = -.5
tangent is negative in the second quadrant or the fourth quadrant.
cosine is negative in the second quadrant and third quadrant.
therefore, if tangent is negative and cosine is negative, the angle has to be in the second quadrant.
if the angle was in the first quadrant, the tangent would be positive.
look for the angle in the first quadrant that has a tangent of .5.
that angle would be equal to 26.56505118 degrees.
the equivalent angle in the second quadrant would be 180 - that = 153.4349488 degrees.
the sine of that would be equal to .4472135953.
that's your solution.
another way:
look at the triangle formed as if it was in the first quadrant.
if the angle is in the first quadrant, than all trigonometric functions are positive.
that means that cotangent is equal to 2.
cotangent is equal to adjacent side / opposite side.
therefore, adjacent side is equal to 2 and opposite side is equal to 1.
by pythagorus, hypotenuse is equal to square root of (adjacent side squared plus opposite side squared).
this makes hypotenuse equal to sqrt(1^2 + 2^2) = sqrt(5).
sine is equal to opposite / hypotenuse which is equal to 1/sqrt(5).
if the angle is in the second quadrant, then the sine is still positive.
decimal equivalent of 1/sqrt(5) is equal to .4472135955.
same answer.
one more way of looking at it.
you have determined that the angle has to be in the second quadrant, and you have determined that cotangent = -2.
this means that adjacent side (represented by x on the unit circle) / opposite side (represented by y in the unit circle) has to be equal to -2.
therefore x is equal to -2 and y is equal to 1 becuse -2/1 = -2.
draw your triangle in the second quadrant.
find the measure of the hypotenuse, which is always positive, by using pythagorus and you get hypotenuse = sqrt(5).
solve for sine to get sine= 1/sqrt(5).
here's the diagram of the unit circle with your triangle formed in the second quadranat.
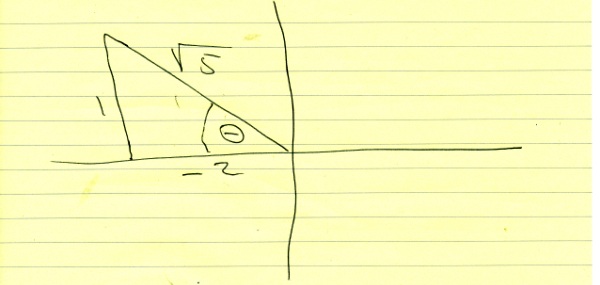
the adjacent side of the angle is the x-coordinate.
the opposite side of the angle is the y-coordinate.
cotangent theta = adjacent / opposite = -2/1 = -2, as required.
cosine theta = adjacent / hypotenuse = -2/sqrt(5) = negative as required.
sine theta = opposite / hypotenuse = 1/sqrt(5) = .4472135955 as we found above.
|
|
|
| |