Question 1099591: if alpha,beta,gamma,and delta(symbols) are the roots of x^4-2x^3+4x^2+6x-21=0 if alpha + beta =0, solve the equation completely.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
if alpha,beta,gamma,and delta(symbols) are the roots of x^4-2x^3+4x^2+6x-21=0 if alpha + beta =0, solve the equation completely.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will use "p" and "q" instead of  and and  to make my writing easier.
So, I am given that p and q are the roots of the equation to make my writing easier.
So, I am given that p and q are the roots of the equation
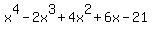 = 0,
such that p = -q. Then the fact that p and q are the roots means = 0,
such that p = -q. Then the fact that p and q are the roots means
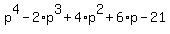 = 0, (1) and = 0, (1) and
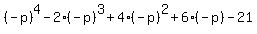 = 0, (2), or = 0, (2), or
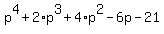 = 0. (3)
Now subtract eq(1) from eq(3) (both sides). You will get = 0. (3)
Now subtract eq(1) from eq(3) (both sides). You will get
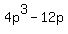 = 0, or = 0, or
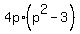 = 0.
It implies that p = +/- = 0.
It implies that p = +/-  .
Thus two roots of the given polynomial are .
Thus two roots of the given polynomial are  and and  .
Then the polynomial is divisible by .
Then the polynomial is divisible by  = =  .
The quotient is .
The quotient is 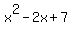 .
The roots of the last quadratic polynomial are .
The roots of the last quadratic polynomial are 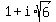 and and  .
Thus the roots of the original polynomial are .
Thus the roots of the original polynomial are  , ,  , , 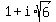 and and  . .
Solved.
|
|
|